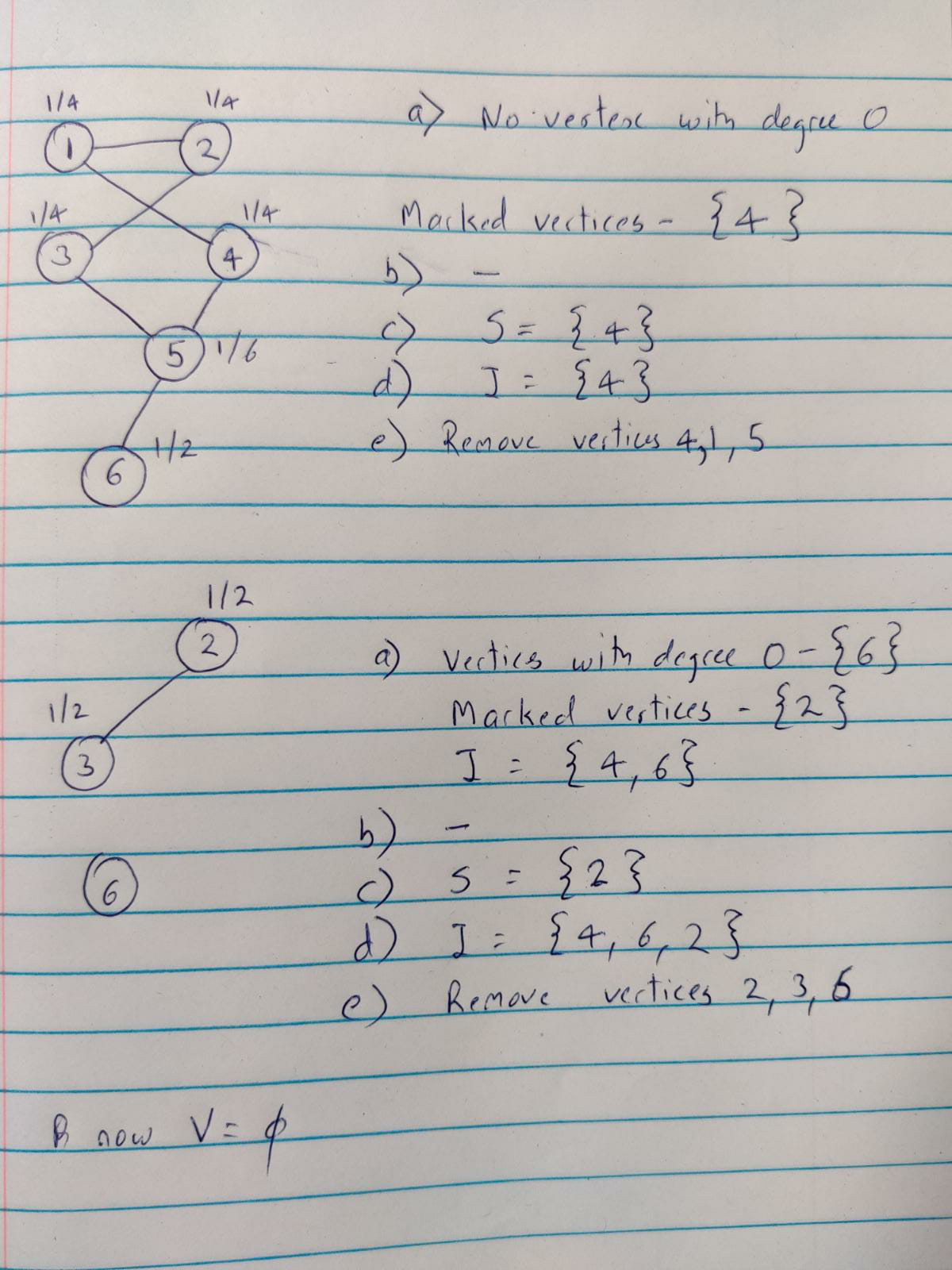2022-03-02
Mar 2 In-Class Exercise.
Please post your solutions to the Mar. 2 In-Class Exercise to this thread.
Best,
Chris
Please post your solutions to the Mar. 2 In-Class Exercise to this thread.
Best,
Chris
((resource:Screen Shot 2022-03-02 at 5.20.33 PM.jpg|Resource Description for Screen Shot 2022-03-02 at 5.20.33 PM.jpg))
Probability based marking is done by random number generator.
Probability based marking is done by random number generator.
((resource:PXL_20220303_012152738.jpg|Resource Description for PXL_20220303_012152738.jpg))
((resource:IMG_0048.jpg|Resource Description for IMG_0048.jpg))
((resource:IMG_8003.jpg|Resource Description for IMG_8003.jpg))
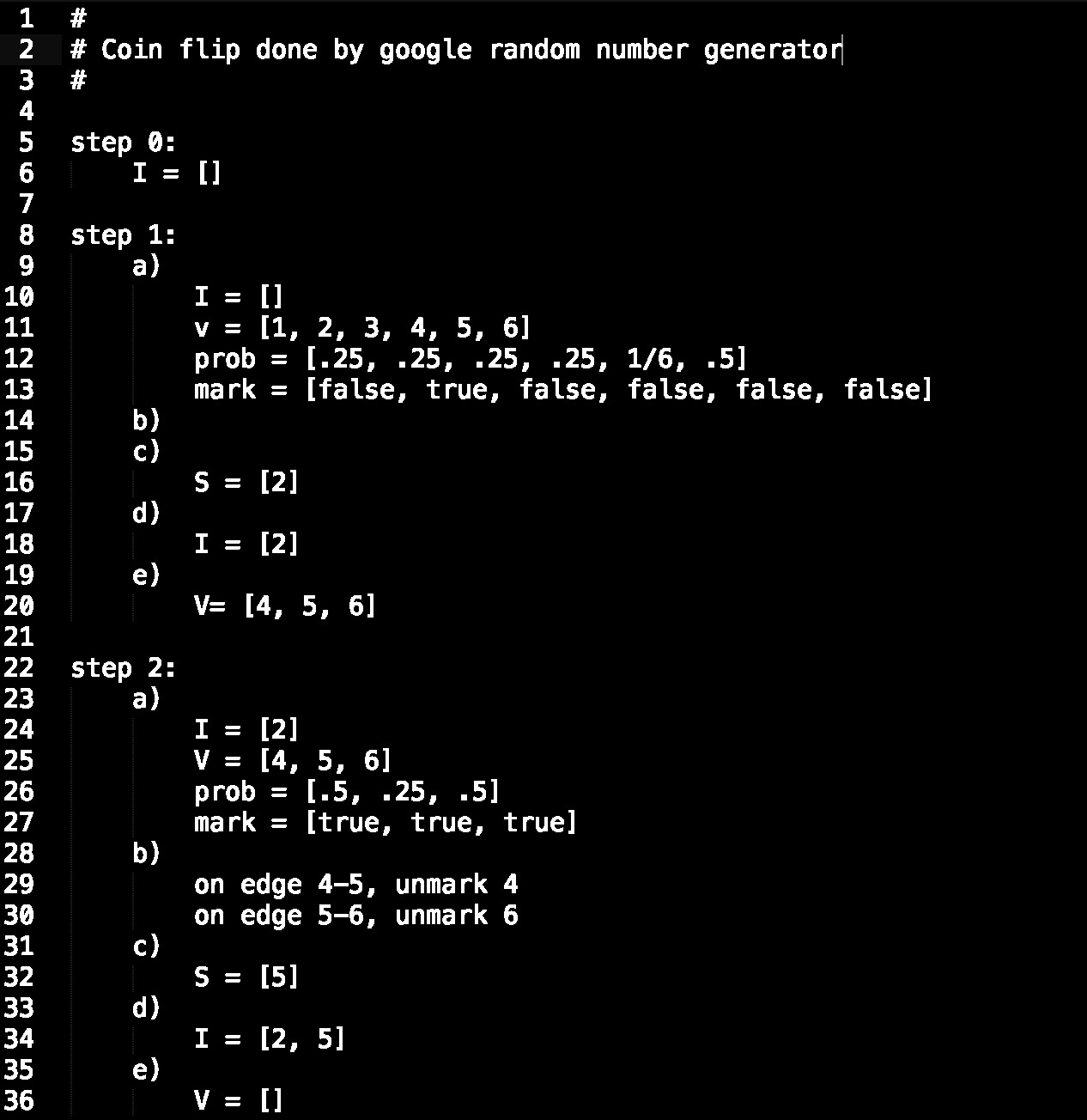
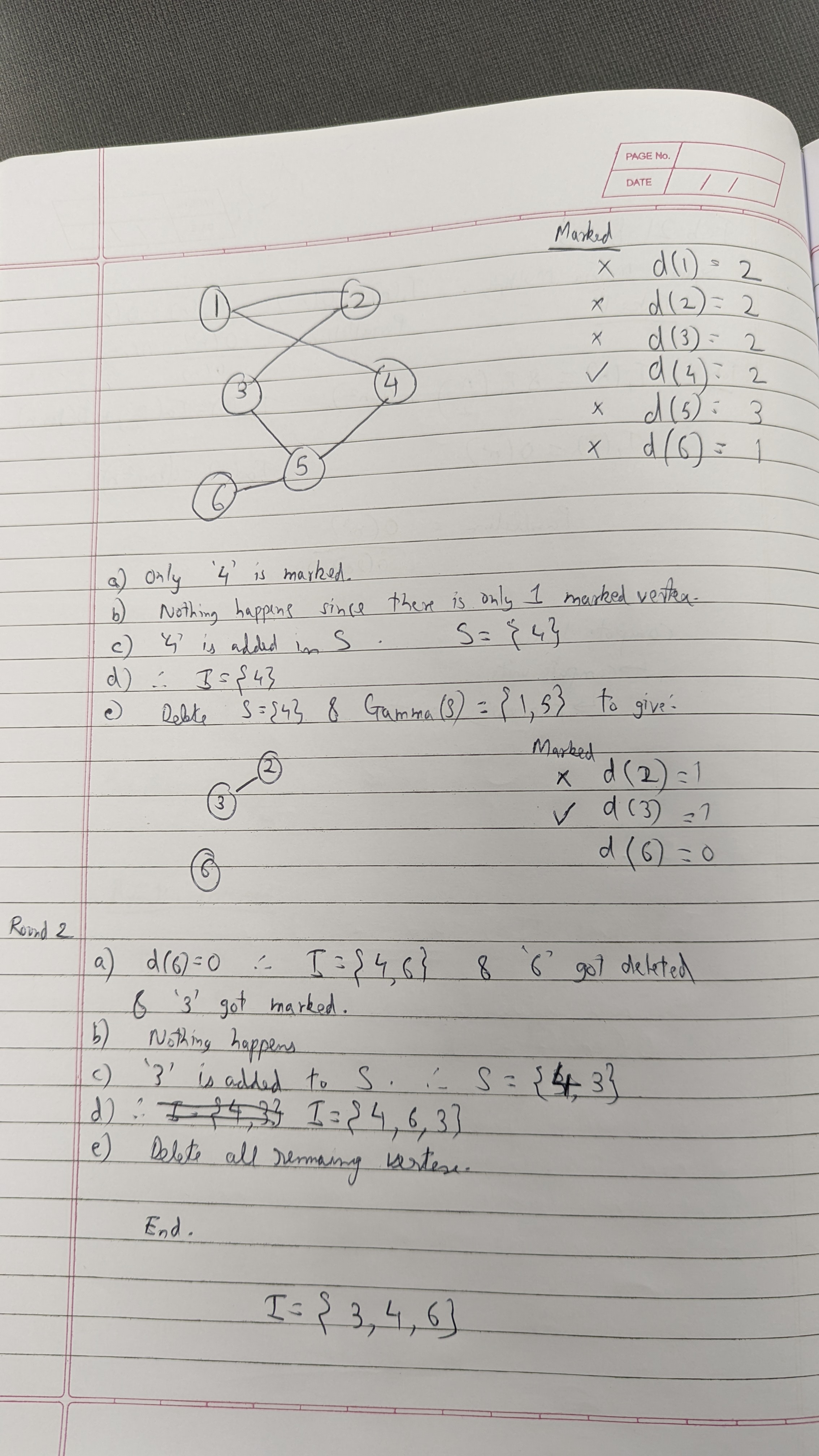
In my experiment, I start off with all vertices. Vertices 1-4 had probability 1/4 to be marked. Vertex 5 had 1/6 probability to be marked. Vertex 6 has probability 1, so it will be marked. After coin tosses, I only had vertex 6 marked. There was no need to unmark since vertex 6 was the only marked vertex. I add it to the union set I and remove 6 and its neighbor 5 from the V set, as well as its edge.
I = {6}
Vertices 1 and 2 had probability 1/4 while vertices 3 and 4 had probability of 1 so it will be marked. After coin tosses, I had vertices 3 and 4 marked. When unmarking, they both had degree 1, so I unmark vertex 3 as it is lexicographically lower. I add vertex 4 to I and remove 4 and its neighbor 1 from the V set, as well as its edge.
I={4,6}
Vertices 1 and 2 had probability 1 so it will be marked. When unmarking, they both had degree 1, so I unmark vertex 1 as it is lexicographically lower. I add vertex 2 to I and remove 2 and its neighbor 1 from the V set, making V empty.
Resulting set is I={3,4,6}.
(Edited: 2022-03-02) In my experiment, I start off with all vertices. Vertices 1-4 had probability 1/4 to be marked. Vertex 5 had 1/6 probability to be marked. Vertex 6 has probability 1, so it will be marked. After coin tosses, I only had vertex 6 marked. There was no need to unmark since vertex 6 was the only marked vertex. I add it to the union set I and remove 6 and its neighbor 5 from the V set, as well as its edge.
I = {6}
Vertices 1 and 2 had probability 1/4 while vertices 3 and 4 had probability of 1 so it will be marked. After coin tosses, I had vertices 3 and 4 marked. When unmarking, they both had degree 1, so I unmark vertex 3 as it is lexicographically lower. I add vertex 4 to I and remove 4 and its neighbor 1 from the V set, as well as its edge.
I={4,6}
Vertices 1 and 2 had probability 1 so it will be marked. When unmarking, they both had degree 1, so I unmark vertex 1 as it is lexicographically lower. I add vertex 2 to I and remove 2 and its neighbor 1 from the V set, making V empty.
Resulting set is I={3,4,6}.
((resource:Screenshot 2022-03-02 213138.png|Resource Description for Screenshot 2022-03-02 213138.png))
G = ([1, 2, 3, 4, 5, 6], E=[(1,2), (1,4), (2,3), (3,5), (4, 5), (5,6)]
I = {}
1 -> d(v) = 2 1/(2*2), not marked
2 -> d(v) = 2 1/(2*2), not marked
3 -> d(v) = 2 1/(2*2), marked
4 -> d(v) = 2 1/(2*2), not marked
5 -> d(v) = 3 1/(2*3), not marked
6 -> d(v) = 1 1/(2*1), marked
(1,2) -> both not marked
(1,4) -> both not marked
(2,3) -> both not marked
(3,5) -> both not marked
(4,5) -> both not marked
(5,6) -> both not marked
1 -> not marked
2 -> not marked
3 -> marked Add 3 to S
4 -> not marked
5 -> not marked
6 -> marked Add 6 to S
S = {3,6}
I = I U S = {3,6}
S U Gamma(S) = {3,6,2,5}
E = [1,4], V = [(1,4)]
1 -> d(v) = 1 1/(2*1), not marked
4 -> d(v) = 1 1/(2*1), not marked
(1,4) -> both not marked
1 -> not marked
4 -> not marked
S = {3,6}
I = I U S = {3,6}
S U Gamma(S) = {3,6,2,5}
E = [1,4], V = [(1,4)]
1 -> d(v) = 1 1/(2*1), marked
4 -> d(v) = 2 1/(2*1), not marked
(1,4) -> both not marked
1 -> marked Add 1 to S
4 -> not marked
S = {3,6, 1}
I = I U S = {3,6, 1}
S U Gamma(S) = {3,6,2,5,1,4}
E = [], V = []
S={3,6,1}
(Edited: 2022-03-02) <pre>
G = ([1, 2, 3, 4, 5, 6], E=[(1,2), (1,4), (2,3), (3,5), (4, 5), (5,6)]
I = {}
1 -> d(v) = 2 1/(2*2), not marked
2 -> d(v) = 2 1/(2*2), not marked
3 -> d(v) = 2 1/(2*2), marked
4 -> d(v) = 2 1/(2*2), not marked
5 -> d(v) = 3 1/(2*3), not marked
6 -> d(v) = 1 1/(2*1), marked
(1,2) -> both not marked
(1,4) -> both not marked
(2,3) -> both not marked
(3,5) -> both not marked
(4,5) -> both not marked
(5,6) -> both not marked
1 -> not marked
2 -> not marked
3 -> marked Add 3 to S
4 -> not marked
5 -> not marked
6 -> marked Add 6 to S
S = {3,6}
I = I U S = {3,6}
S U Gamma(S) = {3,6,2,5}
E = [1,4], V = [(1,4)]
1 -> d(v) = 1 1/(2*1), not marked
4 -> d(v) = 1 1/(2*1), not marked
(1,4) -> both not marked
1 -> not marked
4 -> not marked
S = {3,6}
I = I U S = {3,6}
S U Gamma(S) = {3,6,2,5}
E = [1,4], V = [(1,4)]
1 -> d(v) = 1 1/(2*1), marked
4 -> d(v) = 2 1/(2*1), not marked
(1,4) -> both not marked
1 -> marked Add 1 to S
4 -> not marked
S = {3,6, 1}
I = I U S = {3,6, 1}
S U Gamma(S) = {3,6,2,5,1,4}
E = [], V = []
S={3,6,1}
</pre>
((resource:CS255_2.jpeg|Resource Description for CS255_2.jpeg))
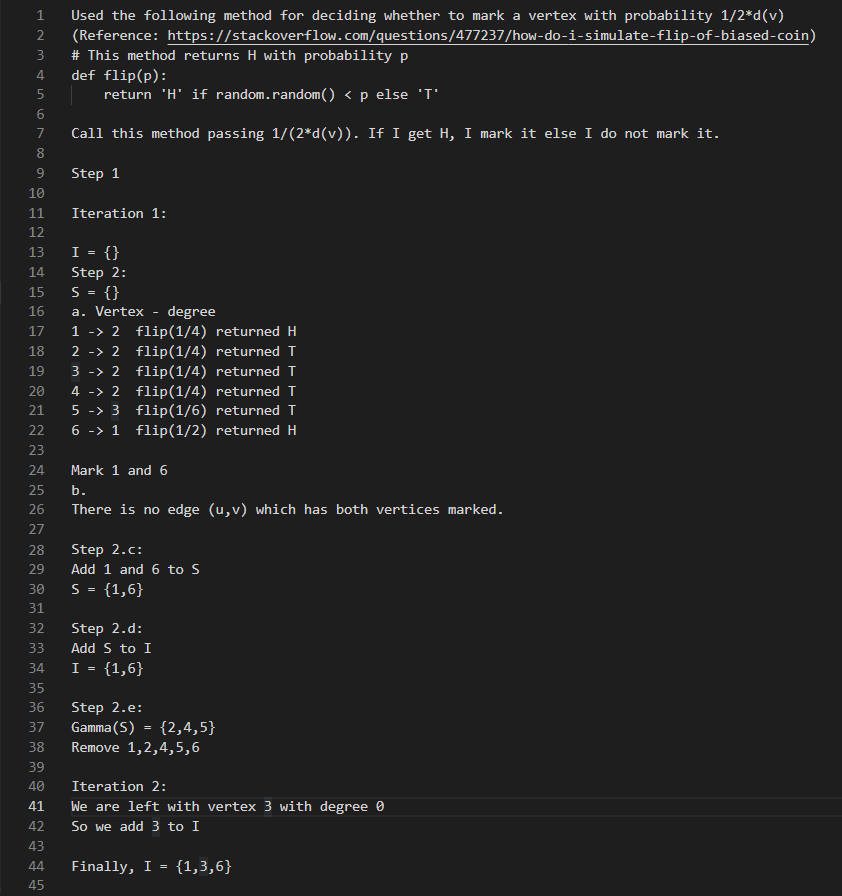
Input: G(V, E), V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
I = maximal independent set, S = internal set
Random generation method: generate number between 1 and 2 * d(n) inclusive, mark if number is 1
1. I = {}, S = {}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
Random Generation: {U, U, M, U, U, M}
2. I = {}, S = {}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
3. I = {}, S = {3, 6}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
4. I = {3, 6}, S = {3, 6}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
Calculation: S union Gamma(S) = {2, 3, 5, 6}
6. I = {3, 6}, S = {3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
Random Generation: {M, U}
7. I = {3, 6}, S = {3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
8. I = {3, 6}, S = {1, 3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
9. I = {1, 3, 6}, S = {1, 3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
Calculation: S union Gamma(S) = {1, 2, 3, 4, 5, 6}
10. I = {1, 3, 6}, S = {1, 3, 6}, V = {}, E = {(4, 5)}
Output: I = {1, 3, 6}
Input: G(V, E), V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
I = maximal independent set, S = internal set
Random generation method: generate number between 1 and 2 * d(n) inclusive, mark if number is 1
1. I = {}, S = {}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
Random Generation: {U, U, M, U, U, M}
2. I = {}, S = {}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
3. I = {}, S = {3, 6}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
4. I = {3, 6}, S = {3, 6}, V = {1, 2, 3, 4, 5, 6}, E = {(1, 2), (1, 4), (2, 3), (3, 5), (4, 5), (5, 6)}
Calculation: S union Gamma(S) = {2, 3, 5, 6}
6. I = {3, 6}, S = {3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
Random Generation: {M, U}
7. I = {3, 6}, S = {3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
8. I = {3, 6}, S = {1, 3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
9. I = {1, 3, 6}, S = {1, 3, 6}, V = {1, 4}, E = {(1, 2), (1, 4), (4, 5)}
Calculation: S union Gamma(S) = {1, 2, 3, 4, 5, 6}
10. I = {1, 3, 6}, S = {1, 3, 6}, V = {}, E = {(4, 5)}
Output: I = {1, 3, 6}
(c) 2025 Yioop - PHP Search Engine