Please post your solutions to the May 1 In-Class Exercise to this thread. Best, Chris

-- May 1 In-Class Exercise

w{1,2} = 3 w{1,3} = 4 w{1,4} = 5 w{2,3} = 5 w{2,4} = 6 w{3,4} = 7 The triangle inequality holds for @BT@w{a,b} <= w{b,c} + w{a,c}@BT@ which equal to @BT@a+b <= a+b+2*c@BT@ minus @BT@a+b@BT@ from both side and @BT@c>0@BT@ @BT@0 <= 2*c@BT@ so edge in this graph obey the triangle inequality

-- May 1 In-Class Exercise

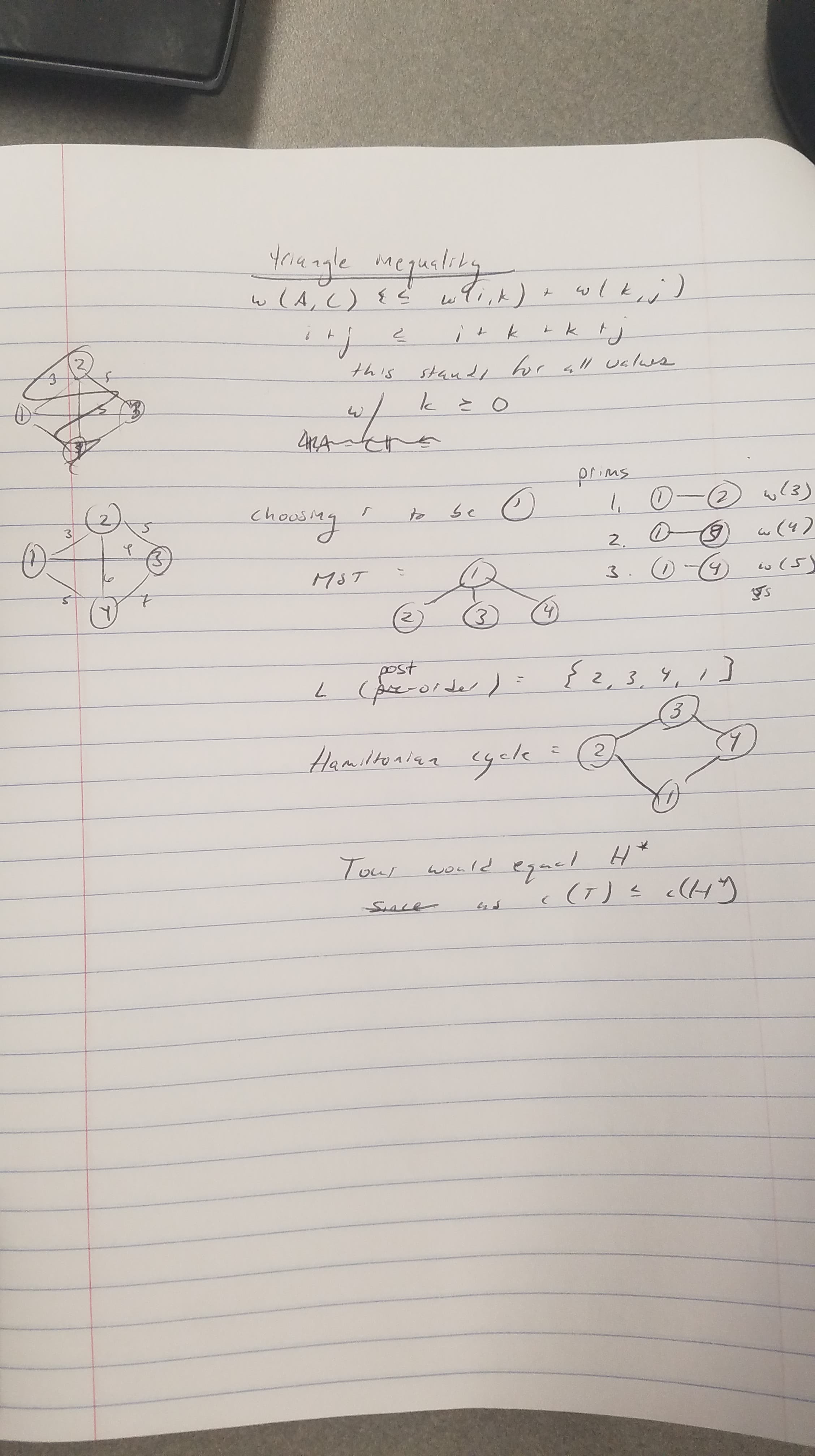
Consider the weighted graph on four vertices @BT@\{1,2,3,4\}@BT@ where the edge weight is computed as the sum of the vertices. So edge @BT@\{1,3\}@BT@ have weight 4. @BT@@BT@ '''Problem:''' Verify that the edges in this graph obey the triangle inequality. @BT@@BT@ '''Solution:''' The triangle inequality states that for any triple of vertices @BT@A, B,@BT@ and @BT@C@BT@, @BT@||A-B|| + ||B-C|| \ge ||A-C||@BT@. For this graph, the triple of vertices @BT@\{1, 2, 3\}@BT@ has edges @BT@\{3, 5, 4\}@BT@ respectively representing the edges from 1 to 2, 2 to 3, and 1 to 3. For the other triples, @BT@\{1, 2, 4\}@BT@ has edges @BT@\{3, 6, 5\}@BT@, @BT@\{1, 3, 4\}@BT@ has edges @BT@\{4, 5, 7\}@BT@ and @BT@\{2, 3, 4\} has edges @BT@\{5, 7, 6\}@BT@. All these triples satisfy the triangle inequality regardless of order. Therefore the graph obeys the triangle inequality. @BT@@BT@ ---- @BT@@BT@ '''Problem:''' Show how the algorithm just given would compute a tour. @BT@@BT@ '''Solution:''' The algorithm would calculate the Minimum Spanning Tree T using Prim’s algorithm, yielding all the edges from vertex 1. The details are as follows: set priorities for each vertex to be infinity and a “prior” variable to be null, then construct a priority queue of all the vertices. Then to build the MST, extract the minimum element from the queue, and update the keys of all adjacent vertices with the minimum of the key value itself and the weight of the edge from the minimum element. Update the prior if the key value is updated. Complete until MST is formed. Then the Hamiltonian cycle of the preorder traversal of the MST formed will be 1, 2, 3, 4.

-- May 1 In-Class Exercise

((resource:58763358_681158642342147_9157244220694593536_n.jpg|Resource Description for 58763358_681158642342147_9157244220694593536_n.jpg))

-- May 1 In-Class Exercise

 The triangle equality states that two sides of a triangle must be equal or greater than the remaining side
 Assume a triangle A, B, C with edge weights as the sum of the values. W(AB) + W(BC) > W(AC) since A + 2B + C > A + C for all positive values.

 MST-Prim
 Choose 1 as the root
 (1,2) (1,3) (1,4)
 Add edge 1,2 (Min weight 3)
 Add edge 1,3 (Min weight 4)
 Add edge 1,4 (Min weight 5)
 So we have 1 as the root and 2,3,4 as the children
 We visit 1 then 2,3,4.

The triangle equality states that two sides of a triangle must be equal or greater than the remaining side Assume a triangle A, B, C with edge weights as the sum of the values. W(AB) + W(BC) > W(AC) since A + 2B + C > A + C for all positive values. MST-Prim Choose 1 as the root (1,2) (1,3) (1,4) Add edge 1,2 (Min weight 3) Add edge 1,3 (Min weight 4) Add edge 1,4 (Min weight 5) So we have 1 as the root and 2,3,4 as the children We visit 1 then 2,3,4.

-- May 1 In-Class Exercise

The edges obey the triangle inequality w(i, j) <= w(i, k) + w(j, k) 
as the weights equal i+j <= i+k + j+k. 
 
Pick 1 as the root vertex.
Compute the MST with Prim's algorithm:
Queue = <(1, 0),(2, inf), (3, inf), (4, inf)>
Pick min = 1
Queue = <(2, 3), (3, 4), (4, 5)>
Pick min = 2
Queue = <(3, 4), (4, 5)>
Pick min = 3
Queue = <(4, 5)>
Pick min = 4 
 
Pre-order traversal: 1,2,3,4 and back to 1 is the tour.

<pre> The edges obey the triangle inequality w(i, j) <= w(i, k) + w(j, k) as the weights equal i+j <= i+k + j+k. Pick 1 as the root vertex. Compute the MST with Prim's algorithm: Queue = <(1, 0),(2, inf), (3, inf), (4, inf)> Pick min = 1 Queue = <(2, 3), (3, 4), (4, 5)> Pick min = 2 Queue = <(3, 4), (4, 5)> Pick min = 3 Queue = <(4, 5)> Pick min = 4 Pre-order traversal: 1,2,3,4 and back to 1 is the tour. </pre>

-- May 1 In-Class Exercise

1. The triangle-inequality equation states that ||A-B|| + ||B-C|| => ||A-C|| The set {1,2,3,4} is a set of vertices with the labels are also the weights. We see that for an equation w(A,B) <= w(A,C) + w(C,B), this equation always hold true since we can break the equation into A+B = (A+C) + (C + B). The RH equation contains the terms of the LH equation, the equation holds true as long as weight of C is > 0. 2. Select v1 as the root. Compute the minimal span of the graph using Prim's algorithm. It will generate the MSP 1->2, 1->3, 1->4 Perform a pre-order treewalk of the MSP: 2,3,4,1 Return the Hamiltonian cycle of the treewalk (2,3,4,1)

-- May 1 In-Class Exercise

there are 6 edges: lengths are 3,4,5, 5, 6, 7. Triangle inequality requires that sum of any two edges' lengths >= any other edge. In our case, two shortest edges' length sum = 3+4 = 7 >= 5,6,7, let alone when edge lengths increase from here. hence triangle inequality holds. Initially, Q = {(1, inf), (2, inf), (3, inf), (4, inf) } , randomly choose 1 as root, update Q to Q = {(1, 0), (2, inf), (3, inf), (4, inf) }, remove 1 from Q, updated Q = { (2, 3), (3, 4), (4, 5)}, update Q = { (3,4), (4,5)} since no weights updated for 3 and 4. Remove 3 and Q = {(4,5)}. So the tree looks like 1 ( root) - 2 (left child) - 3 (middle child) - 4( right child), so post order traverse is 2-3-4-1.

-- May 1 In-Class Exercise

   1. Create a priority Q = {(1,0), (2, infty), (3, infty), (4, infty)}

   2. Pop the min value from Q, then calculate the key, we got Q = {(2,3), (3,4), (4,5)}

   3. Repeat the step 2, we got Q = {(3,4), (4,5)}, then Q = {(4,5)}

w(i,j) <= w(i,k) + w(k, j) i+j <= i + k + k + j i+j <= 2k + i + j k >= 0 In the graph {1,2,3,4}, every vertices >= 0, so the edges in this graph obey the triangle inequality. 1) select vertex 1 to be a root vertex 2) compute the minimal spanning tree tree as following 1. Create a priority Q = {(1,0), (2, infty), (3, infty), (4, infty)} 2. Pop the min value from Q, then calculate the key, we got Q = {(2,3), (3,4), (4,5)} 3. Repeat the step 2, we got Q = {(3,4), (4,5)}, then Q = {(4,5)} 3) Do preorder travel of the tree, we got Hamiltonian cycle 1,2,3,4

-- May 1 In-Class Exercise

1. prove obey triangle inequalities w(v_i, v_j) = v_i + v_j w(v_j, v_k) = v_j + v_k w(v_i, v_k) = v_i + v_k Therefore, w(v_i, v_j) + w(v_j, v_k) > w(v_i, v_k). Triangle inequality proved. 2. Follow the algorithm. (1)Pick 1 a the root vertex. (2)compute MST using Prim's. For vertex 1, 1's key = 0; 1's pi = Nil. For all other vertices, x's key = infinity. x's pi = Nil. Make a priority queue Q. Extract-Min, get vertex 1. Update other vertices' keys and parents. 2's key = 3. 2's pi = 1. 3's key = 4. 3's pi = 1. 4's key = 5. 4's pi = 1. Then, extract-min again. Extract 2. because key(2) + w(2, 3) = 3 + 5 > key(3), key(2) + w(2, 4) > key(4) no updates. Then extract-min, we get 3. key(3) + w(3, 4) > key(4). No updates. Extract-min extracts 4 in the last step. Then it gets empty. MST looks like this: 1 is the root, 2,3,4 are 1's children. (3) vertices listed in pre-order walk of MST: 1, 2, 3, 4. (4) Ham-cycle goes like this, 1->2, 2->3, 3->4, 4->1. A tour is computed.