2019-05-02
2019-05-05
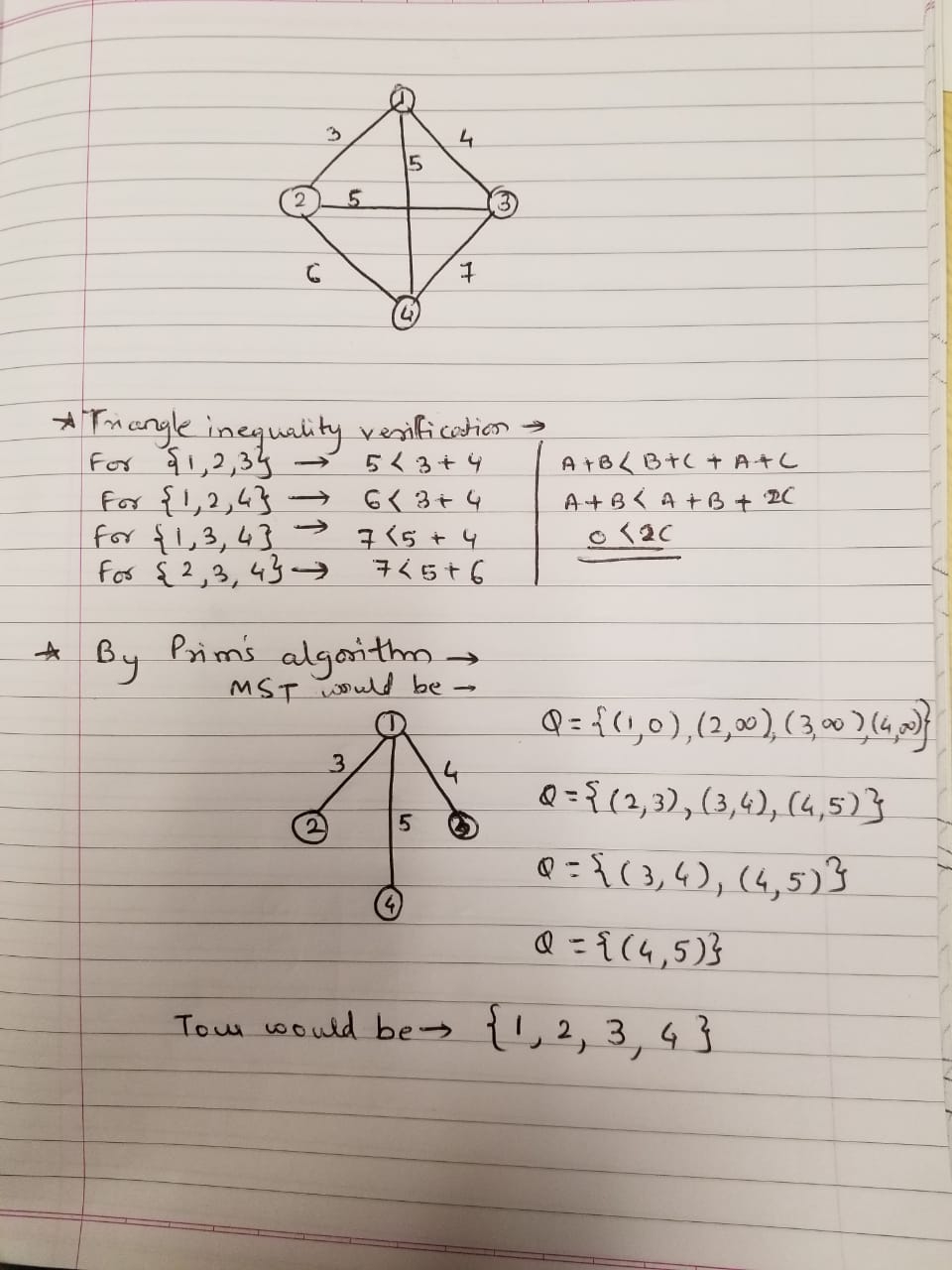
Q: Verify that the edges in this graph obey the triangle inequality
Triangle inequality states for triangle A, B, C, W(AB) + W(BC) > W(AC). The problems states the weight of edge is computed as the sum of the vertices. We have (A+B) + (B+C) > (A+C) is true for all A, B, C. Thus, the graph obey the triangle inequality.
Q: Show how the algorithm just given would compute a tour.
Create priority queue Q = {(1, 0),(2, inf), (3, inf), (4, inf)}.
Choose min=1.
Q={(2, 3), (3, 4), (4, 5)}.
Choose min=2.
Q={(3, 4), (4, 5)}.
Choose min=3.
Q={(4, 5)}.
Choose min=4.
We get pre-order traverse and get 1, 2, 3, 4.
'''Q: Verify that the edges in this graph obey the triangle inequality'''
Triangle inequality states for triangle A, B, C, W(AB) + W(BC) > W(AC). The problems states the weight of edge is computed as the sum of the vertices. We have (A+B) + (B+C) > (A+C) is true for all A, B, C. Thus, the graph obey the triangle inequality.
'''Q: Show how the algorithm just given would compute a tour.'''
Create priority queue Q = {(1, 0),(2, inf), (3, inf), (4, inf)}.
Choose min=1.
Q={(2, 3), (3, 4), (4, 5)}.
Choose min=2.
Q={(3, 4), (4, 5)}.
Choose min=3.
Q={(4, 5)}.
Choose min=4.
We get pre-order traverse and get 1, 2, 3, 4.
1)
w(i,j) <= w(i,k) + w(k,j)
i + j <= i + k + k + j
i + j <= i+ j + 2k
Thus the triangle inequality holds for integers i, j, k > 0
i, j, k will always be three different numbers chosen from {1,2,3,4} for our graph. These are all positive integers so the triangle inequality will hold for all edges.
2)
Pick r = 1
Use Prim's algorithm to compute a minimal spanning tree
Priority queue:
- Q = { (1, 0), (2, inf), (3, inf), (4, inf) }
- Q = { (2, 3), (3, 4), (4, 5) }
- Q = { (3, 4), (4, 5) }
- Q = { (4, 5) }
Do pre-order traversal: 1 -> 2 -> 3 -> 4 -> 1
This is a Hamiltonian cycle.
(Edited: 2019-05-06) '''1) '''
w(i,j) <= w(i,k) + w(k,j)
i + j <= i + k + k + j
i + j <= i+ j + 2k
Thus the triangle inequality holds for integers i, j, k > 0
i, j, k will always be three different numbers chosen from {1,2,3,4} for our graph. These are all positive integers so the triangle inequality will hold for all edges.
'''2) '''
Pick r = 1
Use Prim's algorithm to compute a minimal spanning tree
Priority queue:
* Q = { (1, 0), (2, inf), (3, inf), (4, inf) }
* Q = { (2, 3), (3, 4), (4, 5) }
* Q = { (3, 4), (4, 5) }
* Q = { (4, 5) }
Do pre-order traversal: 1 -> 2 -> 3 -> 4 -> 1
This is a Hamiltonian cycle.
1. For this graph, we can check if the triangle inequality is true by seeing if for any set of three edges, the sum of any of the two should be greater than the third edge.
Since the weight of each edge is calculated by i+j, where i and j are vertices, then assuming that we have three vertices i, j, k, then i+j will always be less than [(i+k) + (j+k)], unless any of i,j or k are less than 1, which is not possible in our problem.
2. Then we can use Prim's algorithm to compute the minimal spanning tree by first constructing a priority queue of all vertices. We traverse this vertex to vertex, removing edges once we have visited them and before we move.
So our queue would look like,
{(1,0), (2,inf), (3,inf), (4,inf)}
{(2,3), (3,4), (4,5)}
{(3,4), (4,5)}
{(4,5)}
We go from 1 -> 2 -> 3 -> 4 -> 1, so in this case it is a Hamiltonian cycle.
1. For this graph, we can check if the triangle inequality is true by seeing if for any set of three edges, the sum of any of the two should be greater than the third edge.
Since the weight of each edge is calculated by i+j, where i and j are vertices, then assuming that we have three vertices i, j, k, then i+j will always be less than [(i+k) + (j+k)], unless any of i,j or k are less than 1, which is not possible in our problem.
2. Then we can use Prim's algorithm to compute the minimal spanning tree by first constructing a priority queue of all vertices. We traverse this vertex to vertex, removing edges once we have visited them and before we move.
So our queue would look like,
{(1,0), (2,inf), (3,inf), (4,inf)}
{(2,3), (3,4), (4,5)}
{(3,4), (4,5)}
{(4,5)}
We go from 1 -> 2 -> 3 -> 4 -> 1, so in this case it is a Hamiltonian cycle.
w(i,j) <= w(i,k) + w(k, j)
i+j <= i + k + k + j
i+j <= 2k + i + j
k >= 0
Thus the triangle inequality holds for integers i, j, k > 0
so edge in this graph obey the triangle inequality
Queue = <(1, 0),(2, inf), (3, inf), (4, inf)>
Queue = <(2, 3), (3, 4), (4, 5)>
Queue = <(3, 4), (4, 5)>
Queue = <(4, 5)>
Pick min = 1 => 2 => 3 => 4 => 1
It's a Hamiltonian cycle.
(Edited: 2019-05-06) w(i,j) <= w(i,k) + w(k, j)
i+j <= i + k + k + j
i+j <= 2k + i + j
k >= 0
Thus the triangle inequality holds for integers i, j, k > 0
so edge in this graph obey the triangle inequality
Queue = <(1, 0),(2, inf), (3, inf), (4, inf)>
Queue = <(2, 3), (3, 4), (4, 5)>
Queue = <(3, 4), (4, 5)>
Queue = <(4, 5)>
Pick min = 1 => 2 => 3 => 4 => 1
It's a Hamiltonian cycle.
2019-05-06
1. To consider w(i,j) <= w(i,k) + w(k,j), the weights would look like i + j <= i + k + k + j. Since the sum of the weights for the other 2 sides also include i + j, it can be shown that the triangle inequality will always hold.
2. First create a priority queue with {(1, 0), (2, inf), (3, inf), (4, inf)}
Then the minimal spanning tree of the queue would look:
- Q = {(2, 3), (3, 4), (4, 5)}
- Q = {(3, 4), (4, 5)}
- Q = {(4, 5)}
Then the pre-order traversal would go 1 -> 2 -> 3 -> 4 -> 1 to compute the tour
1. To consider w(i,j) <= w(i,k) + w(k,j), the weights would look like i + j <= i + k + k + j. Since the sum of the weights for the other 2 sides also include i + j, it can be shown that the triangle inequality will always hold.
2. First create a priority queue with {(1, 0), (2, inf), (3, inf), (4, inf)}
Then the minimal spanning tree of the queue would look:
* Q = {(2, 3), (3, 4), (4, 5)}
* Q = {(3, 4), (4, 5)}
* Q = {(4, 5)}
Then the pre-order traversal would go 1 -> 2 -> 3 -> 4 -> 1 to compute the tour
The triangle inequality holds for w{a,b}≤w{b,c}+w{a,c}
which equal to a+b≤a+b+2⋅c
minus a+b from both side and c>0
0≤2⋅c
MST-Prim Choose 1 as the root (1,2) (1,3) (1,4) Add edge 1,2 Add edge 1,3 Add edge 1,4 We visit 1 then 2,3,4.
The triangle inequality holds for w{a,b}≤w{b,c}+w{a,c}
which equal to a+b≤a+b+2⋅c
minus a+b from both side and c>0
0≤2⋅c
MST-Prim
Choose 1 as the root
(1,2) (1,3) (1,4)
Add edge 1,2
Add edge 1,3
Add edge 1,4
We visit 1 then 2,3,4.
(c) 2025 Yioop - PHP Search Engine