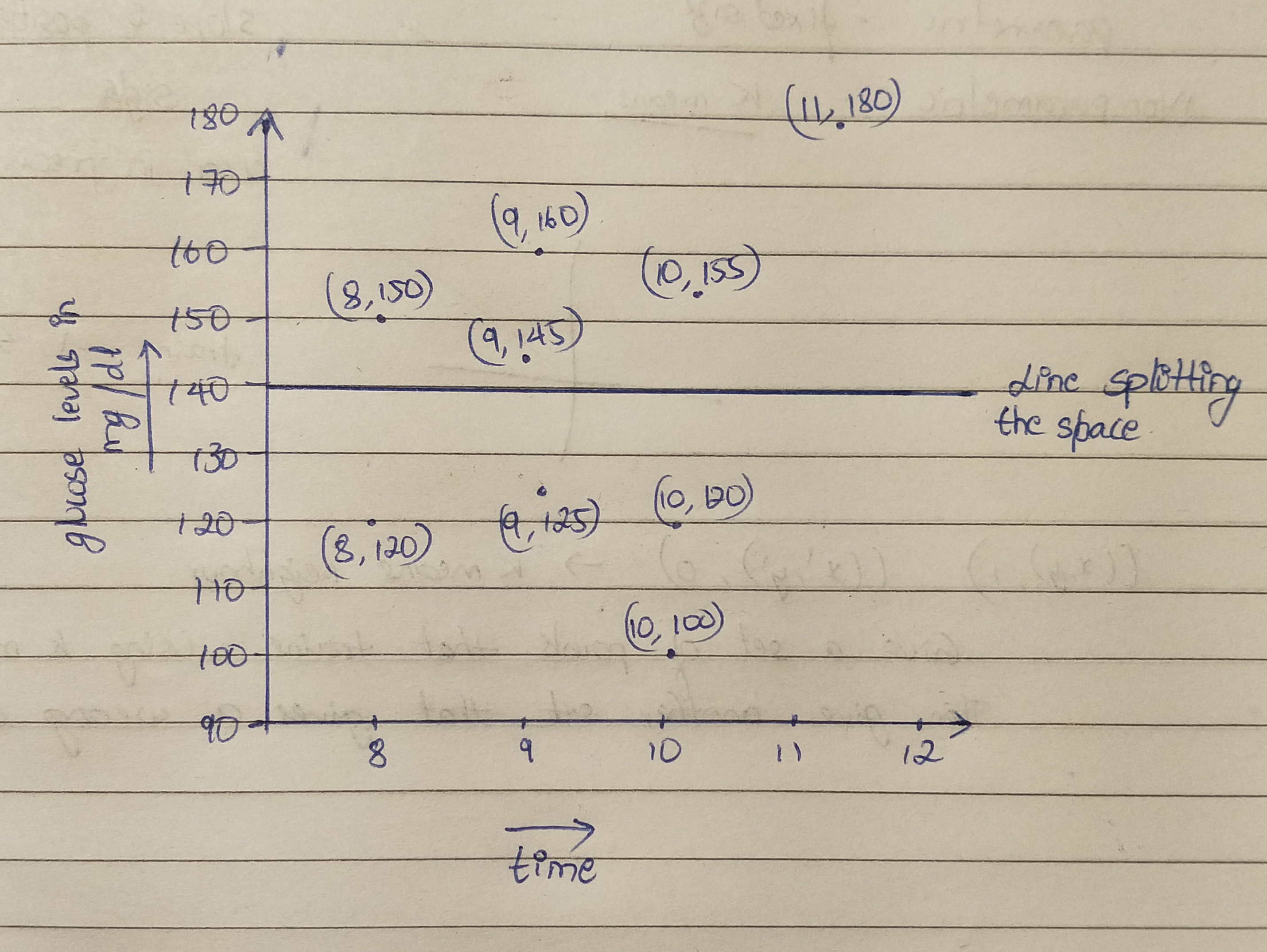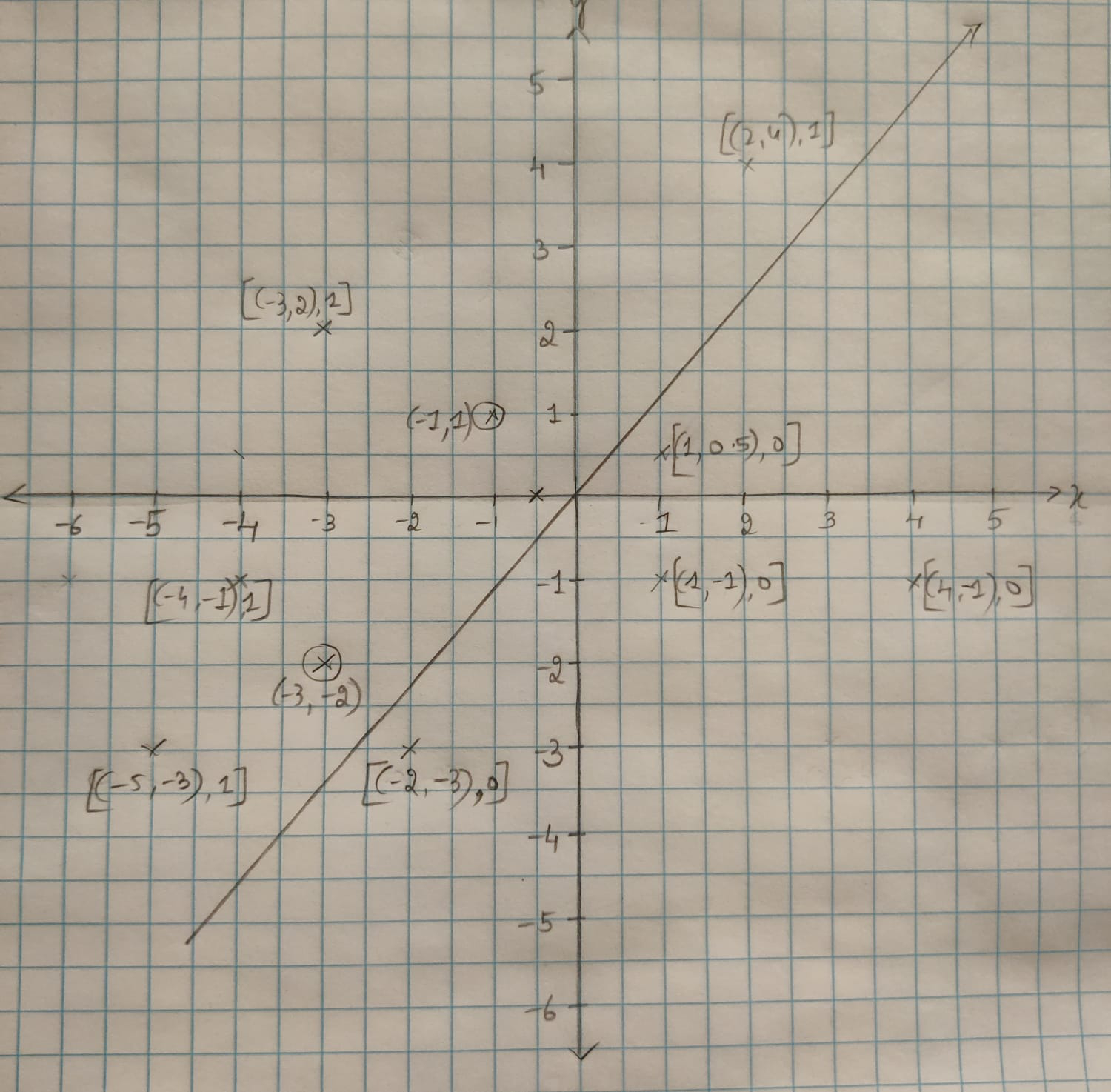2021-08-24
Aug 25 In-Class Exercise .
Please post your solutions to the Aug 25 In-Class Exercise to this thread.
Best,
Chris
Please post your solutions to the Aug 25 In-Class Exercise to this thread.
Best,
Chris
2021-08-27
In-Class Exercise Solution
answer-
Using the distance between two points I can determine the position of the point on the half-plane, and using k nearest neighbors I can determine the probability of finding a point in an area. This approach will be successful for high-density point areas but will not work for low-density outliers. Let's understand this with an example for both a correct and incorrect result situation-
Correct result situation -
Following are the training dataset input - ((7,5),1),((7,4),1),((7,3),1),((7,2),1),((7,1),1), ((0,4),0),((1,4),0),((2,4),0),((3,4),0),((4,4),0),((8,4),0),((9,4),0)
Here the (x,y) coordinates represent a position on the plane and 1 or 0 is the target result of existence of a point at that position, 1 being true and 0 being false.
As you can see in the above training dataset that when the value of x coordinate is at 7, the point appears on the plane, but in all other cases it does not. Therefore it is safe to assume that we have found a high-density K-nearest neighbor points in the region of x distance 7 on the plane and the trained model returns a value of 1 for any input data set having the x coordinate as 7. An example of a correct result would be for a new input (7,8) returning a result of 1. Now let's discuss where an incorrect result would be returned.
Incorrect result situation -
As our trained model believes x coordinate 7 to be a high-density k-nearest neighbor region, it is bound to return a result of 1 with such input. But the model is not trained for input with a negative -y coordinate inputs, as their position is below the line of plane . Therefore if an input of (7,-5) is passed an incorrect result of 1 is produced for a region that never really had any points.
Therefore above the line of the plane, the points exist at x coordinate 7 but below the line of the plane they do not. Therefore an incorrect output is received.
If we parametrically learn this dataset, the smallest model would have been affected by the frequency of outliers in the dataset. For example, a value of ((7,1000),0) is an outlier and their frequency affects the model's attitude towards a high-density area. Making the model's prediction ability weak for even easier predictions.
(Edited: 2021-08-27) <u>'''In-Class Exercise Solution'''</u>
answer-
Using the distance between two points I can determine the position of the point on the half-plane, and using k nearest neighbors I can determine the probability of finding a point in an area. This approach will be successful for high-density point areas but will not work for low-density outliers. Let's understand this with an example for both a correct and incorrect result situation-
'''Correct result situation -'''
Following are the training dataset input - ((7,5),1),((7,4),1),((7,3),1),((7,2),1),((7,1),1), ((0,4),0),((1,4),0),((2,4),0),((3,4),0),((4,4),0),((8,4),0),((9,4),0)
Here the (x,y) coordinates represent a position on the plane and 1 or 0 is the target result of existence of a point at that position, 1 being true and 0 being false.
As you can see in the above training dataset that when the value of '''x coordinate''' is at 7, the point appears on the plane, but in all other cases it does not. Therefore it is safe to assume that we have found a high-density K-nearest neighbor points in the region of x distance 7 on the plane and the trained model returns a value of 1 for any input data set having the x coordinate as 7. An example of a correct result would be for a new input (7,8) returning a result of 1. Now let's discuss where an incorrect result would be returned.
'''Incorrect result situation -'''
As our trained model believes x coordinate 7 to be a high-density k-nearest neighbor region, it is bound to return a result of 1 with such input. But the model is not trained for input with a negative -y coordinate inputs, as their position is '''below the line of plane'''. Therefore if an input of (7,-5) is passed an incorrect result of 1 is produced for a region that never really had any points.
Therefore above the line of the plane, the points exist at x coordinate 7 but below the line of the plane they do not. Therefore an incorrect output is received.
If we parametrically learn this dataset, the smallest model would have been affected by the frequency of outliers in the dataset. For example, a value of ((7,1000),0) is an outlier and their frequency affects the model's attitude towards a high-density area. Making the model's prediction ability weak for even easier predictions.
2021-08-29
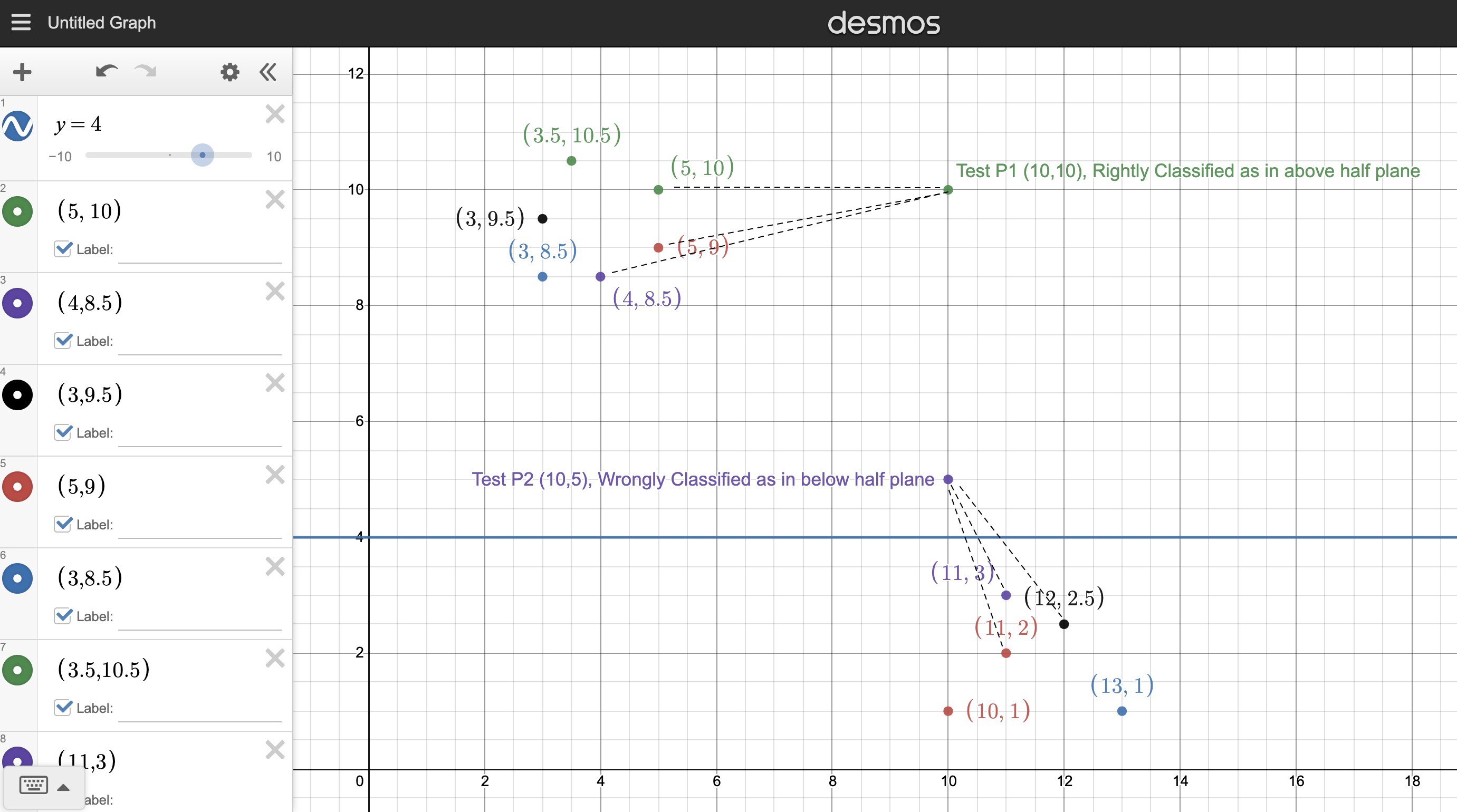
Let the line dividing the half plane be y=4.
Let any point above the line be classified as in the half plane ((x,y),1) and below the line be classified as not in the half plane ((x,y),0)
Let the training set be as shown in the figure.
Let us choose non-parameteric learning classifier as KNN classifier with K=3
Point P1 will be classified as in the half plane, which is correct.
Point P2 will be classified as outside the half plane, (P2,0) since its closer to the points below the line y=4. This classification is wrong since it's above the line in reality and should be classified as (P2,1) .
When choosing a parametric way of learning, when any parameter such as slope of a line which has high precision which cannot be stored in a variable, it may result in inaccurate classification of the test data.
(Edited: 2021-08-29) ((resource:AI CW.jpeg|Resource Description for AI CW.jpeg))
Let the line dividing the half plane be y=4.
Let any point above the line be classified as in the half plane ((x,y),1) and below the line be classified as not in the half plane ((x,y),0)
Let the training set be as shown in the figure.
Let us choose non-parameteric learning classifier as KNN classifier with K=3
'''Point P1 will be classified as in the half plane, which is correct.'''
'''Point P2 will be classified as outside the half plane, (P2,0) since its closer to the points below the line y=4. This classification is wrong since it's above the line in reality and should be classified as (P2,1)'''.
When choosing a parametric way of learning, when any parameter such as slope of a line which has high precision which cannot be stored in a variable, it may result in inaccurate classification of the test data.
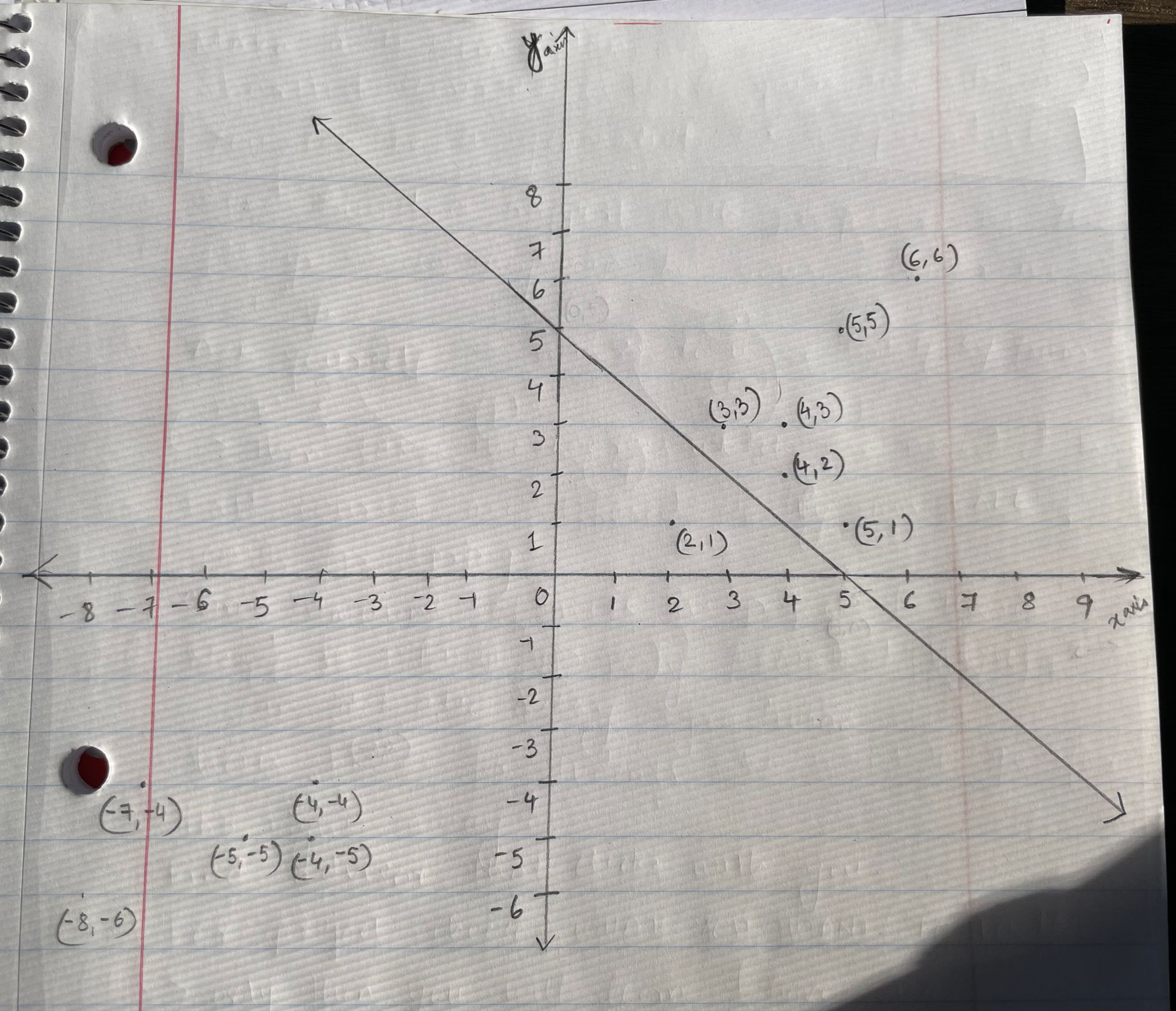
A non-parametric way in which the given space could be learned is k-NN (k nearest neighbors) algorithm. Consider a test dataset ((6,6),1), ((5,5),1), ((3,3),1), ((4,3),1), ((4,2),1), ((-4,-4),0), ((-7,-4),0), ((-5,-5),0), ((-4,-5),0), ((-8,-6),0). Consider k = 3. Attached image shows these points plotted on a graph along with the line that divides the 2D halfspace.
1.Approach produces correct answer:
Take a point (5,1) and use k-NN algorithm. The result produced will be ((5,1),1) i.e. algorithm correctly classifies this point in the halfspace.
2.Approach produces incorrect answer:
Take a point (2,1) and use k-NN algorithm. The result produced will be ((2,1),1) but as the graph indicates, it should ideally be ((2,1),0). This is an example of an incorrect answer.
The problem with using k-NN here is that the slope of the line that divides the 2D space is unknown, so it misclassifies some points on the graph and produces incorrect results.
If we were parametrically learning this dataset, extreme outliers would influence the model.
A non-parametric way in which the given space could be learned is k-NN (k nearest neighbors) algorithm. Consider a test dataset ((6,6),1), ((5,5),1), ((3,3),1), ((4,3),1), ((4,2),1), ((-4,-4),0), ((-7,-4),0), ((-5,-5),0), ((-4,-5),0), ((-8,-6),0). Consider k = 3. Attached image shows these points plotted on a graph along with the line that divides the 2D halfspace.
((resource:In-class exercise graph AI.jpeg|Resource Description for In-class exercise graph AI.jpeg))
1.Approach produces correct answer:
Take a point (5,1) and use k-NN algorithm. The result produced will be ((5,1),1) i.e. algorithm correctly classifies this point in the halfspace.
2.Approach produces incorrect answer:
Take a point (2,1) and use k-NN algorithm. The result produced will be ((2,1),1) but as the graph indicates, it should ideally be ((2,1),0). This is an example of an incorrect answer.
The problem with using k-NN here is that the slope of the line that divides the 2D space is unknown, so it misclassifies some points on the graph and produces incorrect results.
If we were parametrically learning this dataset, extreme outliers would influence the model.
1. A non-parametric way that could be used is k nearest neighbors (example: k=3). A point could be determined if it is in the half space or not depending on its neighbors. I will be considering the line x=0 to determine the half space. All data points with y>0 would be in the half space and y<0 would not be in the half space. I am considering a small dataset with data points ((3,2),1) , ((4,5),1) , ((3,3),1) , ((4,4),1), ((1,-1),0), ((2,-1),0) , ((1,-2),0).
2. Case 1, correct answer: The data point (3,5) is closer to the cluster of points (3,2) , (4,5) , (3,3), (4,4) in the half space, therefore the knn algorithm will classify that point to be in the half space.
Case 2, incorrect answer : The data point (1,1) is in the half space but closer to the data points not in the half space i.e., ((1,-1),(2,-1),(1,-2)), therefore it is incorrectly classified as not being in the half space by the knn algorithm.
3. When using a parametric model, parameters like slope of the line may result in errors for the model. As their precise values need to be stored in a variable, deciding the data type of that variable might affect the classification performance of the model. For example, storing the slope in an integer data type would have a different effect on classification when compared to storing it in a double data type.
(Edited: 2021-08-29) 1. A non-parametric way that could be used is '''k nearest neighbors''' (example: k=3). A point could be determined if it is in the half space or not depending on its neighbors. I will be considering the line x=0 to determine the half space. All data points with y>0 would be in the half space and y<0 would not be in the half space. I am considering a small dataset with data points ((3,2),1) , ((4,5),1) , ((3,3),1) , ((4,4),1), ((1,-1),0), ((2,-1),0) , ((1,-2),0).
2. '''Case 1, correct answer:''' The data point (3,5) is closer to the cluster of points (3,2) , (4,5) , (3,3), (4,4) in the half space, therefore the knn algorithm will classify that point to be in the half space.
'''Case 2, incorrect answer :''' The data point (1,1) is in the half space but closer to the data points not in the half space i.e., ((1,-1),(2,-1),(1,-2)), therefore it is incorrectly classified as not being in the half space by the knn algorithm.
3. When using a parametric model, parameters like slope of the line may result in errors for the model. As their precise values need to be stored in a variable, deciding the data type of that variable might affect the classification performance of the model. For example, storing the slope in an integer data type would have a different effect on classification when compared to storing it in a double data type.
A non parametric way to train the space would be using KNN algorithm.
Suppose for example we are training a basic model to predict the normal range of blood glucose levels plotted against time of the day. We can assume 0 means normal, 1 means above normal and the level of 140 is the line dividing the points into the spaces of normal and high ranges.
We can use the following datasets to train the model :
((8,150),1),((9,160),1),((9,145),1),((10,155)1),((11,180)1),
((8,120)0),((9,125)0),((10,120)0),((10,100)0).
Now with the model trained, if we use test using the data set ((10,180)), then the nearest neighbors would result in 1 predicting that the level is above normal range. This would be the condition where the model predicts the right answer .
However, if we try using the data ((10,1000)) then again the model would predict it to be above the normal range, but in reality such a data set is practically impossible and hence the prediction would be incorrect .
If we are using a parametric model to train this data set, then a lot of parameters would influence the model such as age of the person being tested, the food habits, time of last meal, etc. All these parameters would lead to errors due to their influence on the data and hence would compromise the final predictions of the model.
(Edited: 2021-08-29) ((resource:IMG_20210829_200706.jpg|Resource Description for IMG_20210829_200706.jpg))
A non parametric way to train the space would be using KNN algorithm.
Suppose for example we are training a basic model to predict the normal range of blood glucose levels plotted against time of the day. We can assume 0 means normal, 1 means above normal and the level of 140 is the line dividing the points into the spaces of normal and high ranges.
We can use the following datasets to train the model :
((8,150),1),((9,160),1),((9,145),1),((10,155)1),((11,180)1),
((8,120)0),((9,125)0),((10,120)0),((10,100)0).
Now with the model trained, if we use test using the data set ((10,180)), then the nearest neighbors would result in 1 predicting that the level is above normal range. This would be the condition where the model predicts the '''right answer'''.
However, if we try using the data ((10,1000)) then again the model would predict it to be above the normal range, but in reality such a data set is practically impossible and hence the prediction would be '''incorrect'''.
If we are using a parametric model to train this data set, then a lot of parameters would influence the model such as age of the person being tested, the food habits, time of last meal, etc. All these parameters would lead to errors due to their influence on the data and hence would compromise the final predictions of the model.
- A non-parametric way to learn the 2D half-space is by using k-nearest neighbors. For example, let k = 3 and let the following be our training data: ((0,0),1), ((0,1),1), ((1,1),1) and ((-6,6),0), ((-7,7),0), ((-7,6),0). We are trying to learn the half space by learning the line y = x + 3 where y < x + 3 determines that the point is in the half-space.
- Our approach with the given training data will give correct answer for the test point (-5,5) since its nearest neighbors are the points (-6,6), (-7,7), (-7,6) and hence predicts that the point is not in the half-space ((-5,5),0). But for the point (-2,2) our approach will output ((-2,2),1) since it is closer to (0,0), (0,1), (1,1). This gives incorrect result as the point doesn't lie in the half-space but is incorrectly labelled so.
- If we were using a parametric model, then our accuracy would depend on how precisely our model can figure out the equation of the line y = mx + c. The slope and x-intercept are parameters that need to be stored in a suitable data-type. If we give only 1 bit to these variables, we end up introducing an error. On the other hand allocating more bytes, say for int or double data-type, will increase the precision of the parameters 'm' and 'c' and reduce the error.
#
A non-parametric way to learn the 2D half-space is by using k-nearest neighbors. For example, let k = 3 and let the following be our training data: ((0,0),1), ((0,1),1), ((1,1),1) and ((-6,6),0), ((-7,7),0), ((-7,6),0). We are trying to learn the half space by learning the line y = x + 3 where y < x + 3 determines that the point is in the half-space.
#
Our approach with the given training data will give correct answer for the test point (-5,5) since its nearest neighbors are the points (-6,6), (-7,7), (-7,6) and hence predicts that the point is not in the half-space ((-5,5),0).
But for the point (-2,2) our approach will output ((-2,2),1) since it is closer to (0,0), (0,1), (1,1). This gives incorrect result as the point doesn't lie in the half-space but is incorrectly labelled so.
#
If we were using a parametric model, then our accuracy would depend on how precisely our model can figure out the equation of the line y = mx + c.
The slope and x-intercept are parameters that need to be stored in a suitable data-type. If we give only 1 bit to these variables, we end up introducing an error. On the other hand allocating more bytes, say for int or double data-type, will increase the precision of the parameters 'm' and 'c' and reduce the error.
Assuming we are trying to learn the given half-space using the non-parametric approach of K Nearest Neighbor algorithm. A line passing through the origin separates the 2D half-space, with points above the line being represented as ((x,y), 1) and points below the line represented as ((x,y), 0)
Let’s assume that k=3 i.e., to determine if a point falls above or below the line, we check its three nearest neighbors.
Our test set consists of:
Points (-3,2), (-4,-1), (-5, -3) and (2,4) fall above the line
Points (-2, -3), (4,-1), (1,-1) and (1,0.5) fall below the line
Case for correct answer: Consider the point (-3,-2).
The nearest neighbors for this point are: (-4,-1), (-5,-3) and (-2,-3). The former two points are above the line and the latter below. According to KNN, our point (-2,-2) falls above the line. This is the right answer.
Case for wrong answer: Consider the point (-1,1).
The nearest neighbors for this point are: (1,0.5), (1,-1) which fall below the line and point (-3,2) which falls above the line. Since the majority of neighbors fall below the line, (-1,1) is shown to fall below the line as well, which is incorrect.
If we were trying to learn this data set parametrically, we would need to take into account quantities like slope of the line and position of the points. We need to think about the number of bits needed to represent these quantities. If the number of bits is low, that is, the data type that is used to store these values is not large enough to accommodate the worst case scenarios, for margin for error increases.
(Edited: 2021-08-29) ((resource:aI.jpeg|Resource Description for aI.jpeg))
Assuming we are trying to learn the given half-space using the non-parametric approach of K Nearest Neighbor algorithm. A line passing through the origin separates the 2D half-space, with points above the line being represented as ((x,y), 1) and points below the line represented as ((x,y), 0)
Let’s assume that k=3 i.e., to determine if a point falls above or below the line, we check its three nearest neighbors.
Our test set consists of:
Points (-3,2), (-4,-1), (-5, -3) and (2,4) fall above the line
Points (-2, -3), (4,-1), (1,-1) and (1,0.5) fall below the line
'''Case for correct answer:''' Consider the point (-3,-2).
The nearest neighbors for this point are: (-4,-1), (-5,-3) and (-2,-3). The former two points are above the line and the latter below. According to KNN, our point (-2,-2) falls above the line. This is the right answer.
'''Case for wrong answer:''' Consider the point (-1,1).
The nearest neighbors for this point are: (1,0.5), (1,-1) which fall below the line and point (-3,2) which falls above the line. Since the majority of neighbors fall below the line, (-1,1) is shown to fall below the line as well, which is incorrect.
----
If we were trying to learn this data set parametrically, we would need to take into account quantities like slope of the line and position of the points. We need to think about the number of bits needed to represent these quantities. If the number of bits is low, that is, the data type that is used to store these values is not large enough to accommodate the worst case scenarios, for margin for error increases.
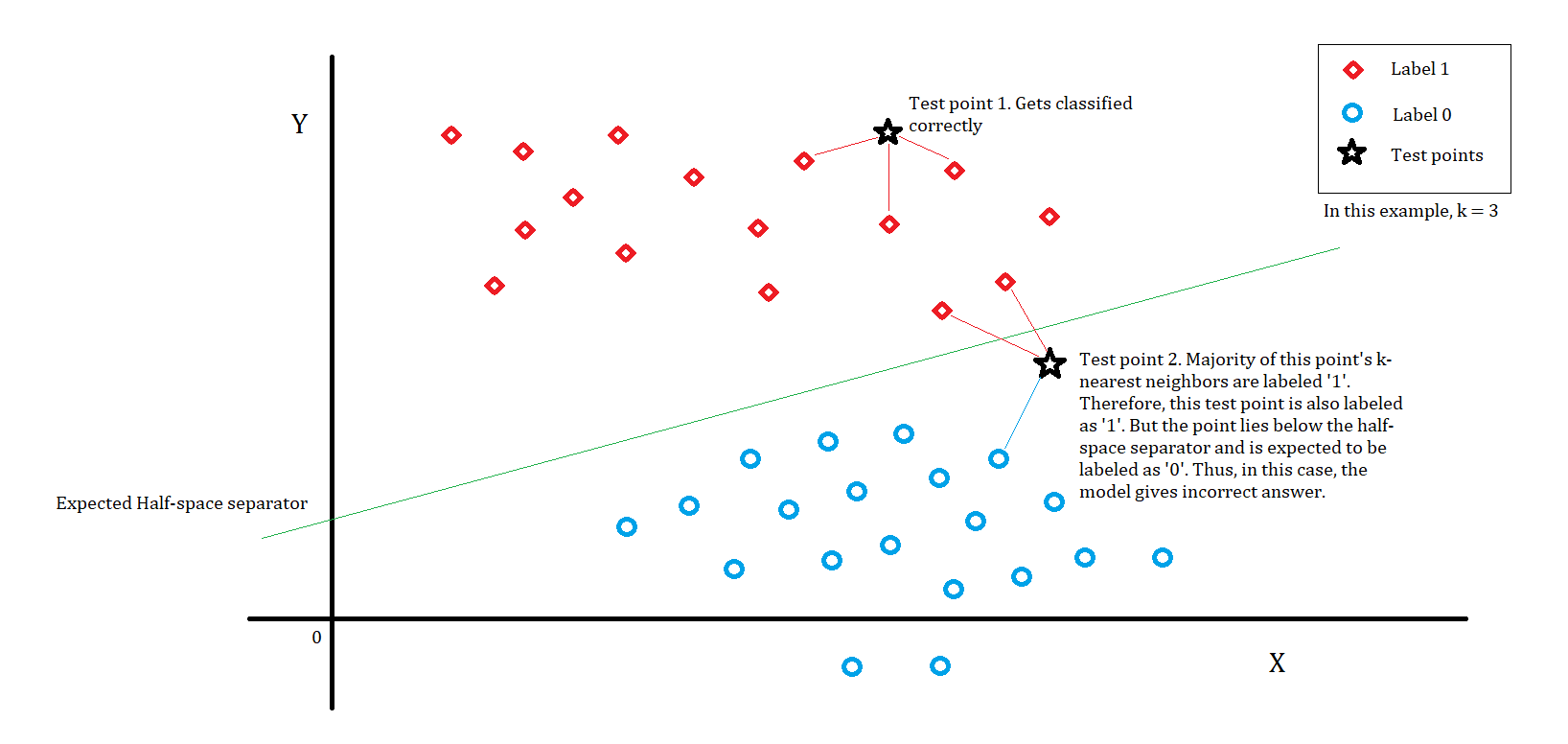
- For the non-parametric learning approach, the ‘k-nearest neighbors’ method is a suitable way. In this way, we can label a test point based on the labels of its neighbors. For example, if we choose k=3 we consider 3 nearest neighbors of the test point. We then see the labels of the chosen nearest neighbors and assign the majority label. If we set the value of k as something greater than 3 (say 5), we would have more contestants to choose the winning label. This may increase the correctness of the solution.
- Consider the following diagram. The diagram shows two types of points. The points having label 1 (red diamonds) are in the top part of the half-space, while the others (blue circles) are in the bottom part of the half-space. The green line is the correct separator of the two parts of the half-space. Our objective is to learn this separator. There are two test points (black stars). The first test point is tightly surrounded by alike labeled points and thus gets the correct label. On the other hand, for test point 2, although the point is below the separator the model incorrectly labels it as 1, because the majority of its k-nearest neighbors were labeled 1.
Suppose we choose k as some even number, then sometimes there may be a tie in the selection of the majority label. So the model may incorrectly label some points.
- If we learn the dataset parametrically, the smallest model possible would consist of parameters such as the slope of the half-space separator line, its y-intercept, and the side of the line that has label 1 (The other side will automatically get label 0). The separator will be of the form y = mx + b where ‘m’ is the slope and ‘b’ is the y-intercept. The correctness of the learned model depends on how precisely we learn this value. The constants 'm' and 'b' are real numbers and they may take values that are impossible to store in memory with full precision. For example, if the slope is some real number having 100 decimal places and we have a limitation to store the value until only a few decimal places, at some point we have to start rounding off. The error produced due to rounding off will reduce the correctness of the model for some points. If we have better storage space, then the error is decreased. Thus the precision of the storage influences the model.
* For the non-parametric learning approach, the ‘k-nearest neighbors’ method is a suitable way. In this way, we can label a test point based on the labels of its neighbors. For example, if we choose k=3 we consider 3 nearest neighbors of the test point. We then see the labels of the chosen nearest neighbors and assign the majority label. If we set the value of k as something greater than 3 (say 5), we would have more contestants to choose the winning label. This may increase the correctness of the solution.
----
* Consider the following diagram. The diagram shows two types of points. The points having label 1 (red diamonds) are in the top part of the half-space, while the others (blue circles) are in the bottom part of the half-space. The green line is the correct separator of the two parts of the half-space. Our objective is to learn this separator. There are two test points (black stars). The first test point is tightly surrounded by alike labeled points and thus gets the correct label. On the other hand, for test point 2, although the point is below the separator the model incorrectly labels it as 1, because the majority of its k-nearest neighbors were labeled 1.
Suppose we choose k as some even number, then sometimes there may be a tie in the selection of the majority label. So the model may incorrectly label some points.
((resource:Knn_inclass.png|Resource Description for Knn_inclass.png))
----
* If we learn the dataset parametrically, the smallest model possible would consist of parameters such as the slope of the half-space separator line, its y-intercept, and the side of the line that has label 1 (The other side will automatically get label 0). The separator will be of the form '''y = mx + b''' where ‘m’ is the slope and ‘b’ is the y-intercept. The correctness of the learned model depends on how precisely we learn this value. The constants 'm' and 'b' are real numbers and they may take values that are impossible to store in memory with full precision. For example, if the slope is some real number having 100 decimal places and we have a limitation to store the value until only a few decimal places, at some point we have to start rounding off. The error produced due to rounding off will reduce the correctness of the model for some points. If we have better storage space, then the error is decreased. Thus the precision of the storage influences the model.
(c) 2026 Yioop - PHP Search Engine