2021-09-21
Sep 22 In-Class Exercise .
Please post your solutions to the Sep 20 In-Class Exercise to this thread.
Best,
Chris
Please post your solutions to the Sep 20 In-Class Exercise to this thread.
Best,
Chris
2021-09-22
Algorithm ->
1. Roughly, sort the points by their x coordinate.
2. Put first half of the points in one set, the rest in the other.
3. Compute convex hulls of the two sub-problems and merge results.
Base case-> Individual points in each set will form the base case.
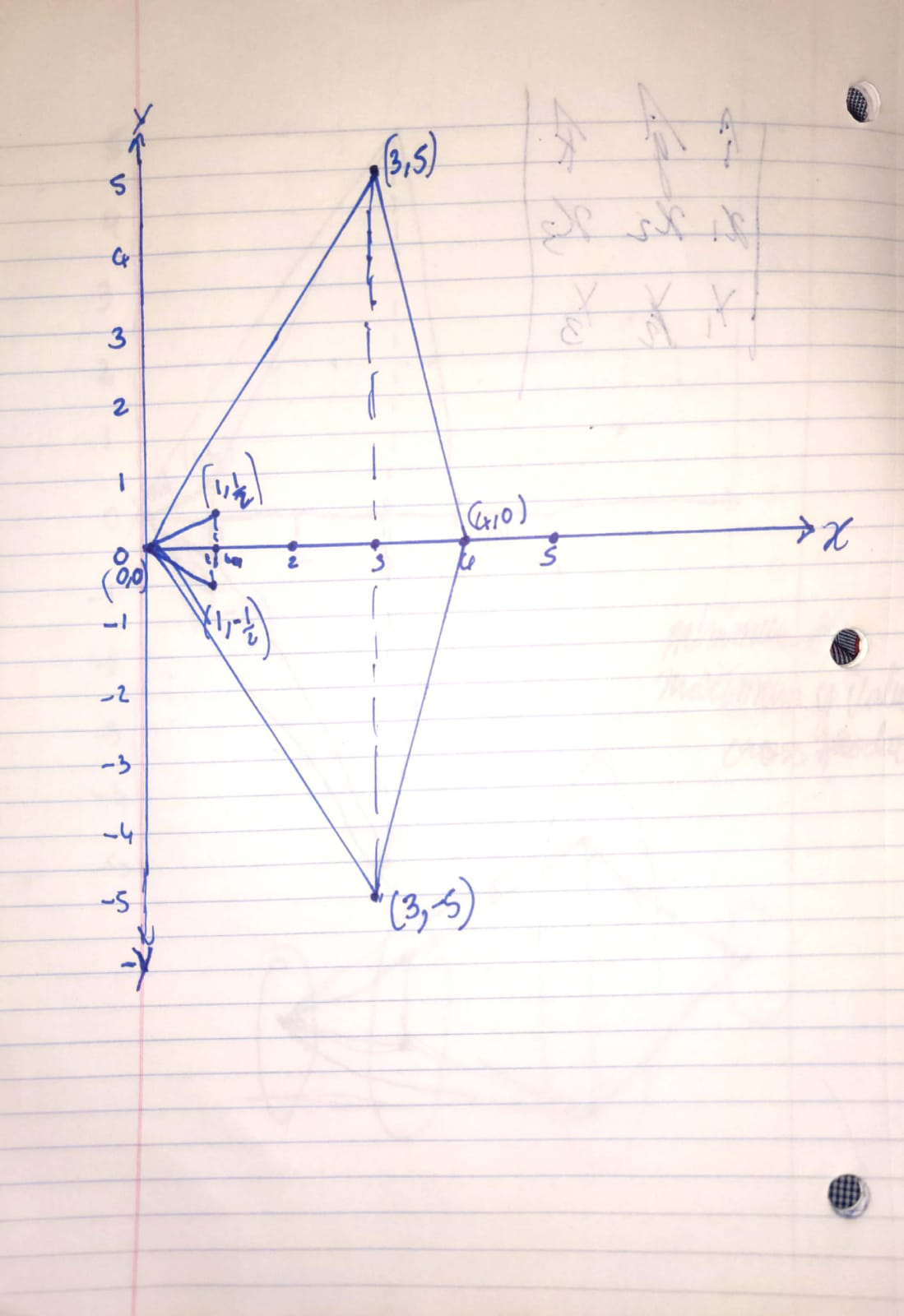
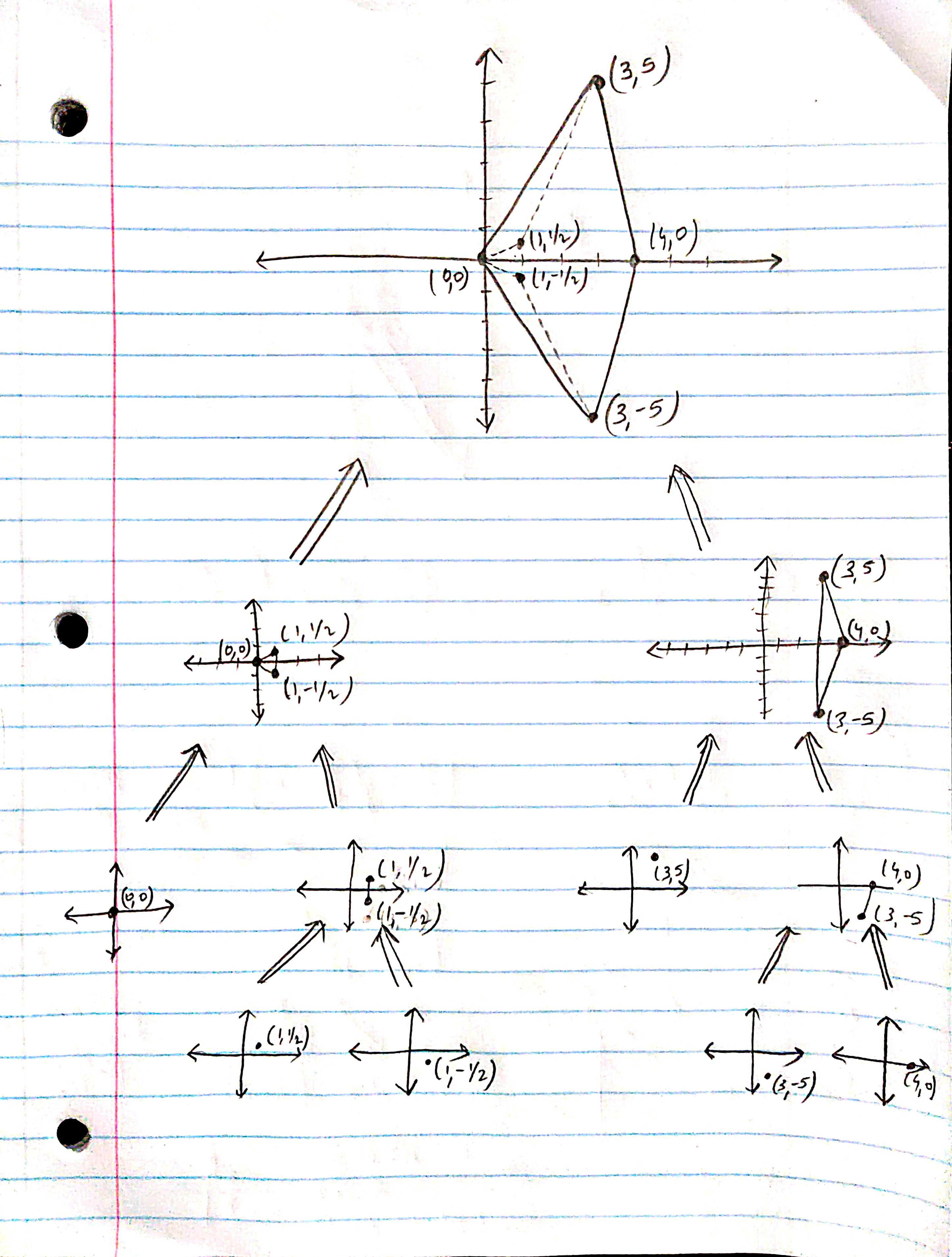
1. Sorting based on x coordinate - Two sets of three points each will form set 1 and set 2. Set 1 consists of {(0,0), (1, ½), (1,-1/2)} and set 2 consists of {(3,5) ,(3,-5), (4,0)}.
2. After recursive splitting of set 1 and 2, we will have (0,0), (1,1/2), (1,-1/2), (3,5), (3,-5), (4,0).
Merging -> As the points are sorted according to x coordinate value, consider the maximum and minimum y coordinate values for merging.
1. First merging will result in 4 sets which are set 1 {(0,0)}, set 2 {(1,1/2), (1,-1/2)} , set 3 {(3,5) , (3,-5)} and set 4 {(4,0)}.
2. Set 1 and 2 will merge to form the left triangle and set 3 and 4 will merge to form the right triangle.
3. For connecting the points from right triangle to the left triangle, first consider (3,5) and (1,1/2). The vector that connects these two points will move outward in clockwise direction (as determined by the cross product) and connect to (0,0).
4. Similarly, the vector that connects (3,-5) and (1,-1/2) will move outward in anticlockwise direction to connect to (0,0).
Finally, the points (0,0), (3,5), (3,-5) and (4,0) form the convex hull.
<u>Algorithm</u> ->
1. Roughly, sort the points by their x coordinate.
2. Put first half of the points in one set, the rest in the other.
3. Compute convex hulls of the two sub-problems and merge results.
<br>
<u>Base case</u>-> Individual points in each set will form the base case.
1. Sorting based on x coordinate - Two sets of three points each will form set 1 and set 2. Set 1 consists of {(0,0), (1, ½), (1,-1/2)} and set 2 consists of {(3,5) ,(3,-5), (4,0)}.
2. After recursive splitting of set 1 and 2, we will have (0,0), (1,1/2), (1,-1/2), (3,5), (3,-5), (4,0).
<br>
<u>Merging</u> -> As the points are sorted according to x coordinate value, consider the maximum and minimum y coordinate values for merging.
1. First merging will result in 4 sets which are set 1 {(0,0)}, set 2 {(1,1/2), (1,-1/2)} , set 3 {(3,5) , (3,-5)} and set 4 {(4,0)}.
2. Set 1 and 2 will merge to form the left triangle and set 3 and 4 will merge to form the right triangle.
3. For connecting the points from right triangle to the left triangle, first consider (3,5) and (1,1/2). The vector that connects these two points will move outward in clockwise direction (as determined by the cross product) and connect to (0,0).
4. Similarly, the vector that connects (3,-5) and (1,-1/2) will move outward in anticlockwise direction to connect to (0,0).
<br>
Finally, the points (0,0), (3,5), (3,-5) and (4,0) form the convex hull.
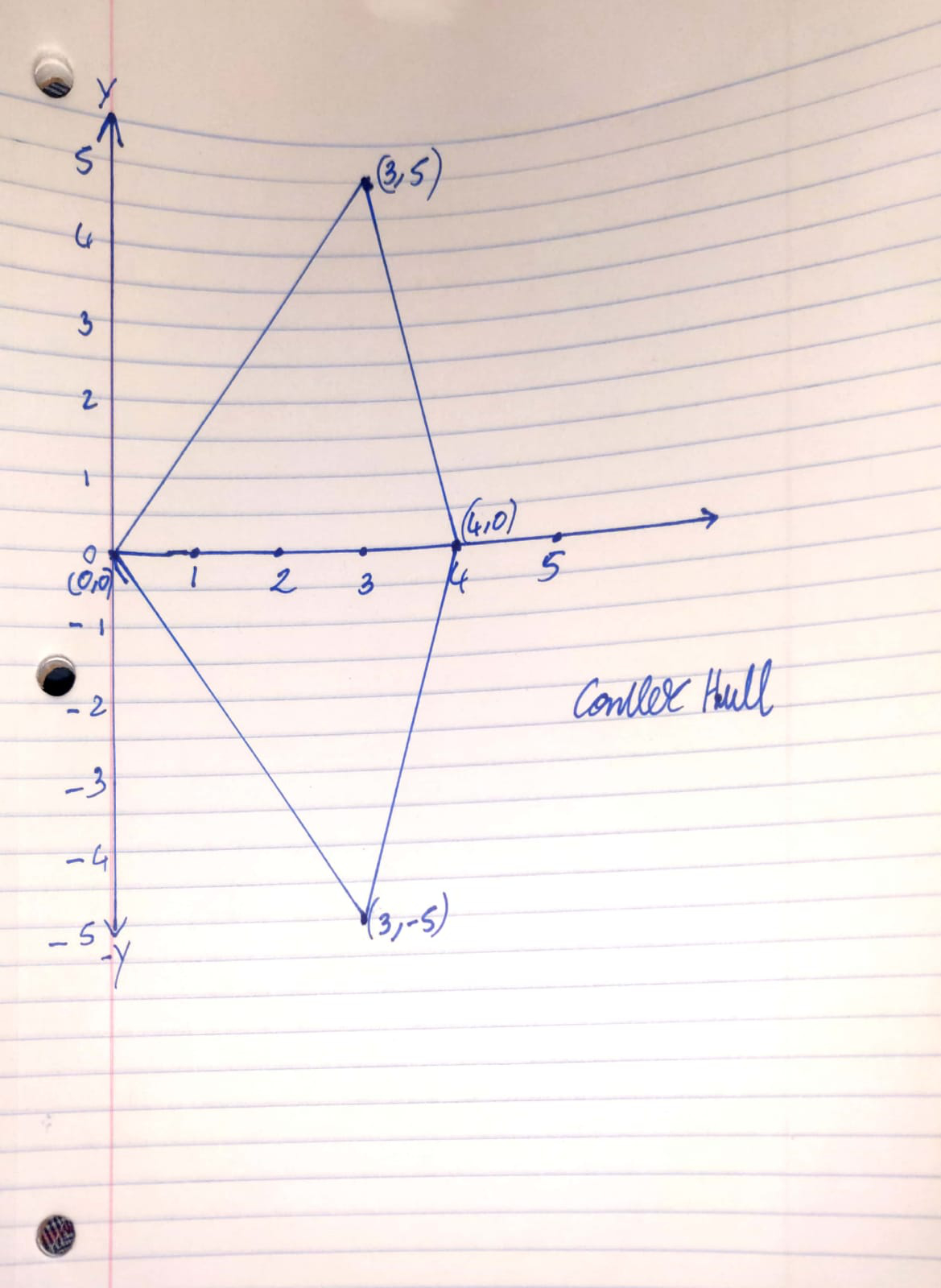
Algorithm: Follow the divide and conquer approach. Split the points into smaller sets till you get individual points.
Base case will be reached when we reach unit pints for all the points.
` {(0,0),(1,1/2),(1,-1/2),(3,5),(3,-5),(4,0)} `
Initially the convex hull of these individual points will be the point itself.
Now draw line segments for each pair of points.
Start with (0,0) as the reference point and take cross product with the next points to determine if there is another point to be included in the result set.
This will give a triangular like shape for the two set of points.
Merge the two and see if a point lies within the convex hull of the combined set, that point can be removed.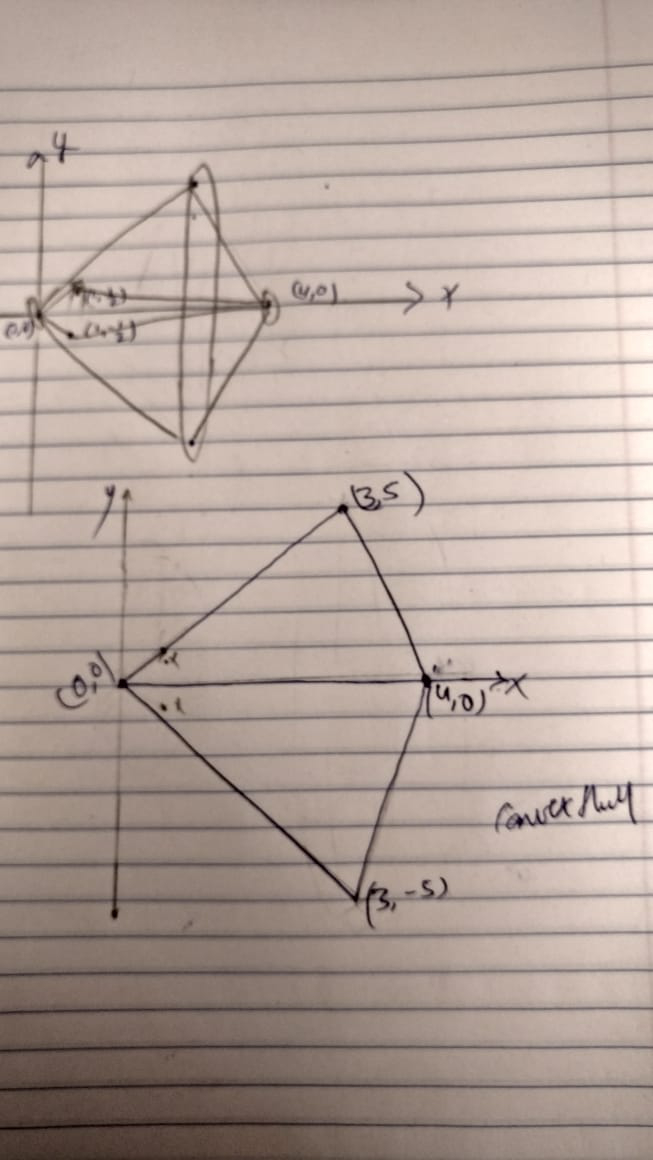

Find the upper limit by checking if a higher value lies on either side of the line. Move towards the max value and take that value in the convex hull for the set.
As shown in the figure we will get convex hull at each step and then merge the two 3 points convex hull to get the final result would include the following points.
convex hull in the end- `{(0,0),(3,5),(3,-5),(4,0)} `
(Edited: 2021-09-23) Algorithm: Follow the divide and conquer approach. Split the points into smaller sets till you get individual points.
Base case will be reached when we reach unit pints for all the points.
@BT@ {(0,0),(1,1/2),(1,-1/2),(3,5),(3,-5),(4,0)} @BT@
Initially the convex hull of these individual points will be the point itself.
Now draw line segments for each pair of points.
Start with (0,0) as the reference point and take cross product with the next points to determine if there is another point to be included in the result set.
This will give a triangular like shape for the two set of points.
Merge the two and see if a point lies within the convex hull of the combined set, that point can be removed.((resource:WhatsApp Image 2021-09-23 at 5.49.27 PM.jpeg|Resource Description for WhatsApp Image 2021-09-23 at 5.49.27 PM.jpeg))
Find the upper limit by checking if a higher value lies on either side of the line. Move towards the max value and take that value in the convex hull for the set.
As shown in the figure we will get convex hull at each step and then merge the two 3 points convex hull to get the final result would include the following points.
convex hull in the end- @BT@{(0,0),(3,5),(3,-5),(4,0)} @BT@
2021-09-25
ALGORITHM
1. First mark all points (0,0),(1,12),(1,−12),(3,5),(3,−5),(4,0) on the plot.
2. Divide first half of the points on one side by drawing lines among them and the other half on the other side.
3. Now using cross products among points find the minimum and maximum value of Y coordinate and draw a convex hull using these new merged computations.
Mainly-
As shown in the above diagram the cross product of points (0,0) and (3,5) give the highest value for Y and therefore is chosen, and the cross product of points (0,0) and (3,-5) gives the minimum value of Y therefore, it is chosen. Together these computations converge to form a Convex Hull.
(Edited: 2021-09-25) ((resource:WhatsApp Image 2021-09-25 at 9.33.01 PM.jpeg|Resource Description for WhatsApp Image 2021-09-25 at 9.33.01 PM.jpeg))
((resource:WhatsApp Image 2021-09-25 at 9.33.19 PM.jpeg|Resource Description for WhatsApp Image 2021-09-25 at 9.33.19 PM.jpeg))
'''ALGORITHM'''
1. First mark all points (0,0),(1,12),(1,−12),(3,5),(3,−5),(4,0) on the plot.
2. Divide first half of the points on one side by drawing lines among them and the other half on the other side.
3. Now using cross products among points find the minimum and maximum value of Y coordinate and draw a convex hull using these new merged computations.
'''Mainly- '''
As shown in the above diagram the cross product of points (0,0) and (3,5) give the highest value for Y and therefore is chosen, and the cross product of points (0,0) and (3,-5) gives the minimum value of Y therefore, it is chosen. Together these computations converge to form a Convex Hull.
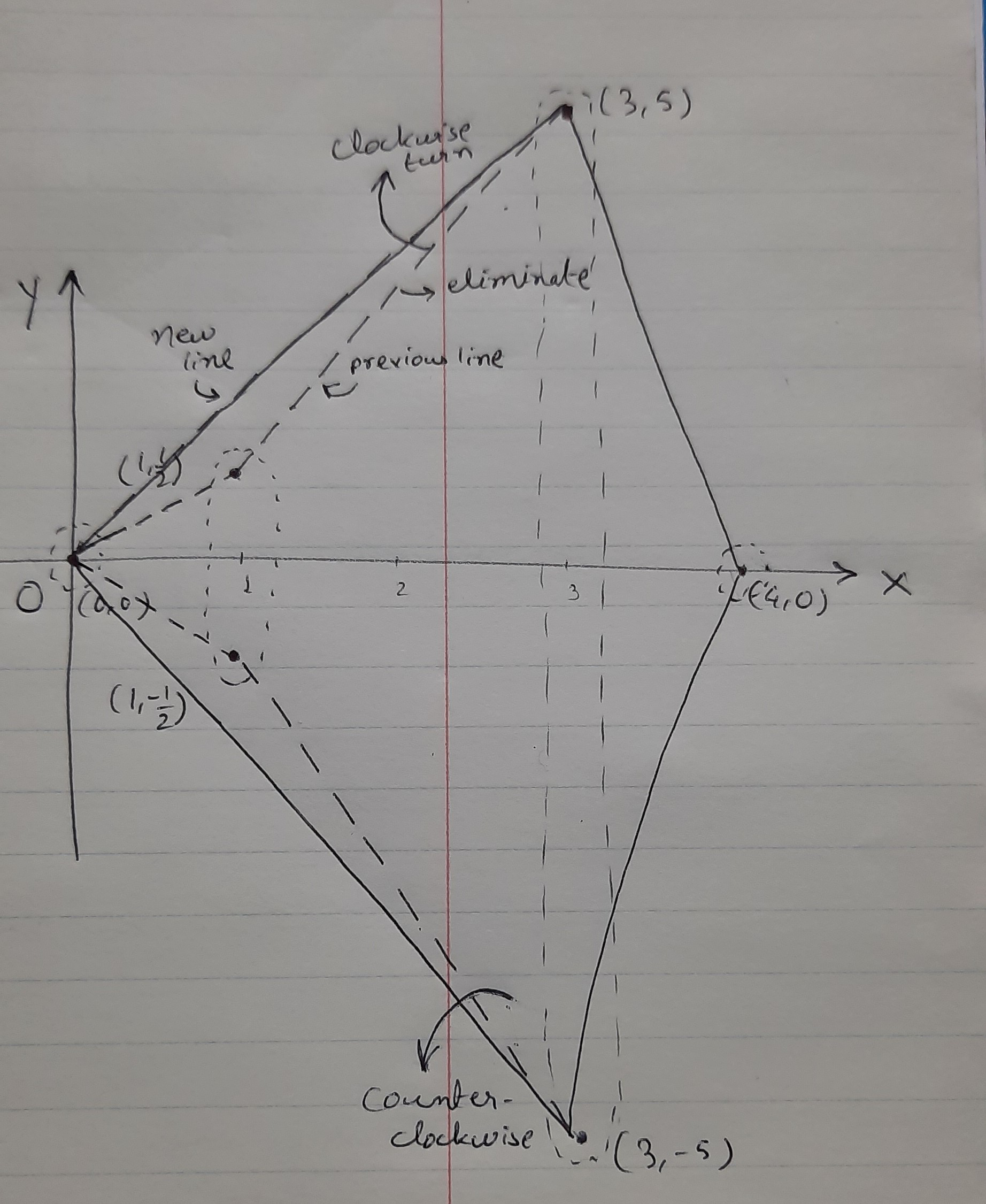
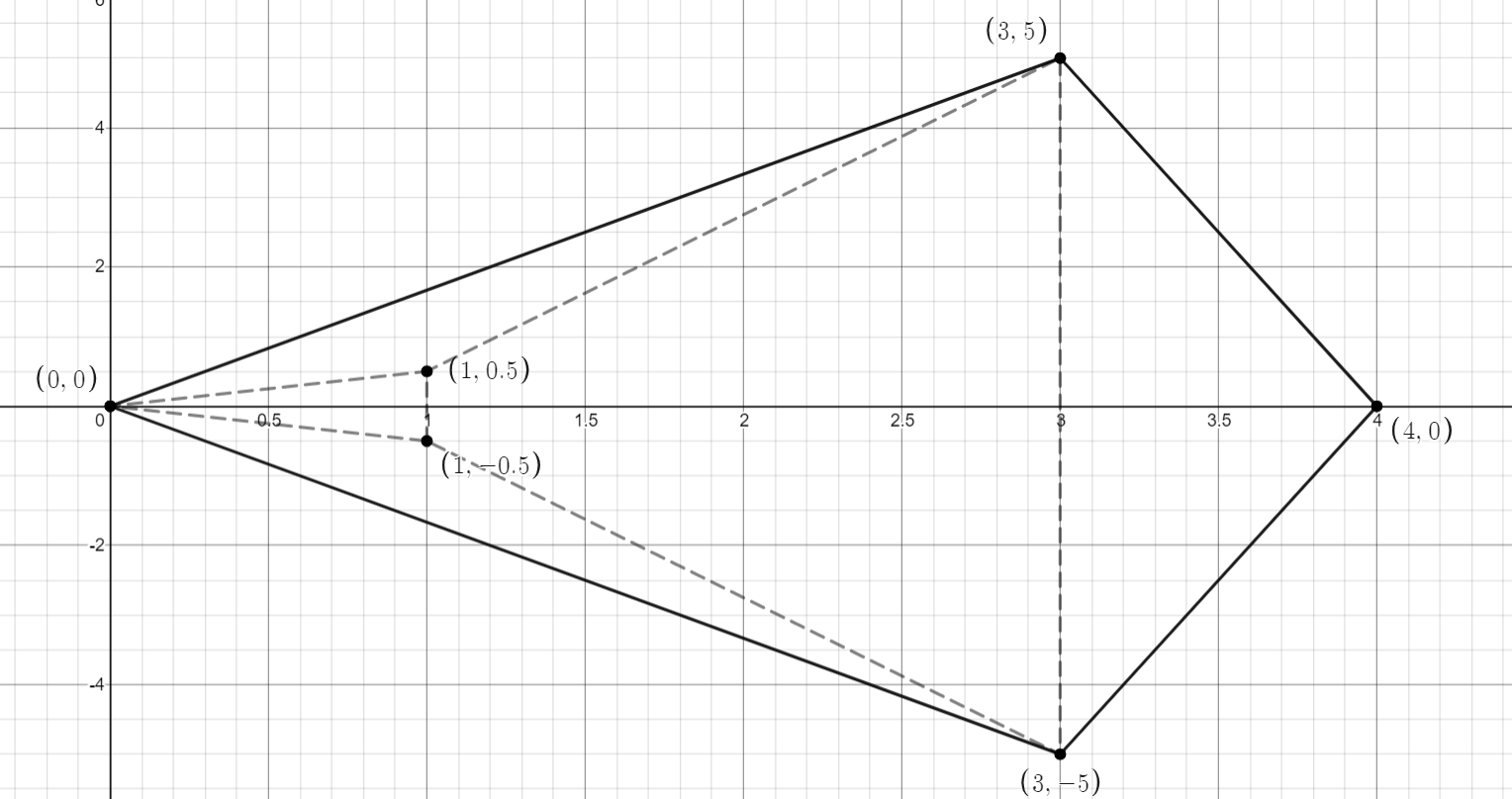
The objective of the exercise was to find the convex hull for the given set of points. The following procedure is applied:
Given points: {(0,0), (1, 0.5), (1, -0.5), (3,5), (3,-5), (4,0)}
- Initially, we sort the points based on their X coordinates. The points that have the same X-coordinates will become the base convex hull sets. Here {(0,0)}, {(1,0.5), (1,-0.5)}, {(3,5),(3,-5)}, {(4,0)} will be the base convex hulls. Now we have to merge them to create one final convex hull.
- We will merge the base sets from left to right based on their X-coordinates. First step will merge the set {(0,0)}. Now we need to merge {(1,0.5), (-1, 0.5)}. We will consider the extreme Y-coordinates, in this case, these points are themselves extremes. Draw a line with extremes of current convex hull set {(0,0)}. Find if there are points behind this point (behind means, having lesser X-coordinate value). If there is, we will find if the line with this point turns 'clockwise' w.r.t the old line (counter-clockwise if the line has a negative slope). If the turn is valid, we will consider this new line for our convex hull and eliminate the previous line.
- The merging will continue until all the points are covered.
The following diagram illustrates the merge process:
The objective of the exercise was to find the convex hull for the given set of points. The following procedure is applied:
Given points: {(0,0), (1, 0.5), (1, -0.5), (3,5), (3,-5), (4,0)}
* Initially, we sort the points based on their X coordinates. The points that have the same X-coordinates will become the base convex hull sets. Here {(0,0)}, {(1,0.5), (1,-0.5)}, {(3,5),(3,-5)}, {(4,0)} will be the base convex hulls. Now we have to merge them to create one final convex hull.
* We will merge the base sets from left to right based on their X-coordinates. First step will merge the set {(0,0)}. Now we need to merge {(1,0.5), (-1, 0.5)}. We will consider the extreme Y-coordinates, in this case, these points are themselves extremes. Draw a line with extremes of current convex hull set {(0,0)}. Find if there are points behind this point (behind means, having lesser X-coordinate value). If there is, we will find if the line with this point turns 'clockwise' w.r.t the old line (counter-clockwise if the line has a negative slope). If the turn is valid, we will consider this new line for our convex hull and eliminate the previous line.
* The merging will continue until all the points are covered.
The following diagram illustrates the merge process:
((resource:AI-inclass-Sept22.jpg|Resource Description for AI-inclass-Sept22.jpg))
The divide and conquer algorithm that will be used has the following steps:
- Sort the points by their x coordinate.
- Put first half of the points in one set and rest in the other set.
- Compute convex hull for these 2 sub-problems and merge.
- This will lead to splitting of points till we reach the base case of a single point where that point in itself is a convex hull.
- The merging is done by firstly, taking the highest Y-coordinate points from both the sets. The vector from the right set's point to the left set's point is considered and then that vector is rotated towards decreasing x-coordinate value (basically getting a positive cross product) to the next point if possible. For lowest Y-coordinate, the increasing X-coordinate (anti-clockwise direction) is used.
- All points encompassed inside these vectors are ignored.
For our given set, we first recursively split the set {(0,0),(1,1/2),(1,−1/2),(3,5),(3,−5),(4,0)} till we get single points. The points (0,0),(1,1/2),(1,−1/2) then get merged to form a triangle on the left and the points (3,5),(3,−5),(4,0) merge into a triangle, which is its convex hull, on the right.
Now we consider the vector from (3,5) to (1,1/2). This can be rotated clockwise to give the vector from (3,5) to (0,0) since their cross product is positive. Similarly, for the negative y-coordinates, vector from (3,-5) to (0,0) is used. This gives us the convex hull for the whole set as: {(0,0),(3,5),(3,−5),(4,0)}
(Edited: 2021-09-26) The divide and conquer algorithm that will be used has the following steps:
* Sort the points by their x coordinate.
* Put first half of the points in one set and rest in the other set.
* Compute convex hull for these 2 sub-problems and merge.
* This will lead to splitting of points till we reach the base case of a single point where that point in itself is a convex hull.
* The merging is done by firstly, taking the highest Y-coordinate points from both the sets. The vector from the right set's point to the left set's point is considered and then that vector is rotated towards decreasing x-coordinate value (basically getting a positive cross product) to the next point if possible. For lowest Y-coordinate, the increasing X-coordinate (anti-clockwise direction) is used.
* All points encompassed inside these vectors are ignored.
For our given set, we first recursively split the set {(0,0),(1,1/2),(1,−1/2),(3,5),(3,−5),(4,0)} till we get single points. The points (0,0),(1,1/2),(1,−1/2) then get merged to form a triangle on the left and the points (3,5),(3,−5),(4,0) merge into a triangle, which is its convex hull, on the right.
Now we consider the vector from (3,5) to (1,1/2). This can be rotated clockwise to give the vector from (3,5) to (0,0) since their cross product is positive. Similarly, for the negative y-coordinates, vector from (3,-5) to (0,0) is used. This gives us the convex hull for the whole set as: {(0,0),(3,5),(3,−5),(4,0)}
((resource:convex hull.jpg|Resource Description for convex hull.jpg))
2021-09-26
(Edited: 2021-09-26)
((resource:AI in-class exercise sep 22 (1).jpeg|Resource Description for AI in-class exercise sep 22 (1).jpeg))
((resource:AI in-class exercise sep 22 (2).jpeg|Resource Description for AI in-class exercise sep 22 (2).jpeg))
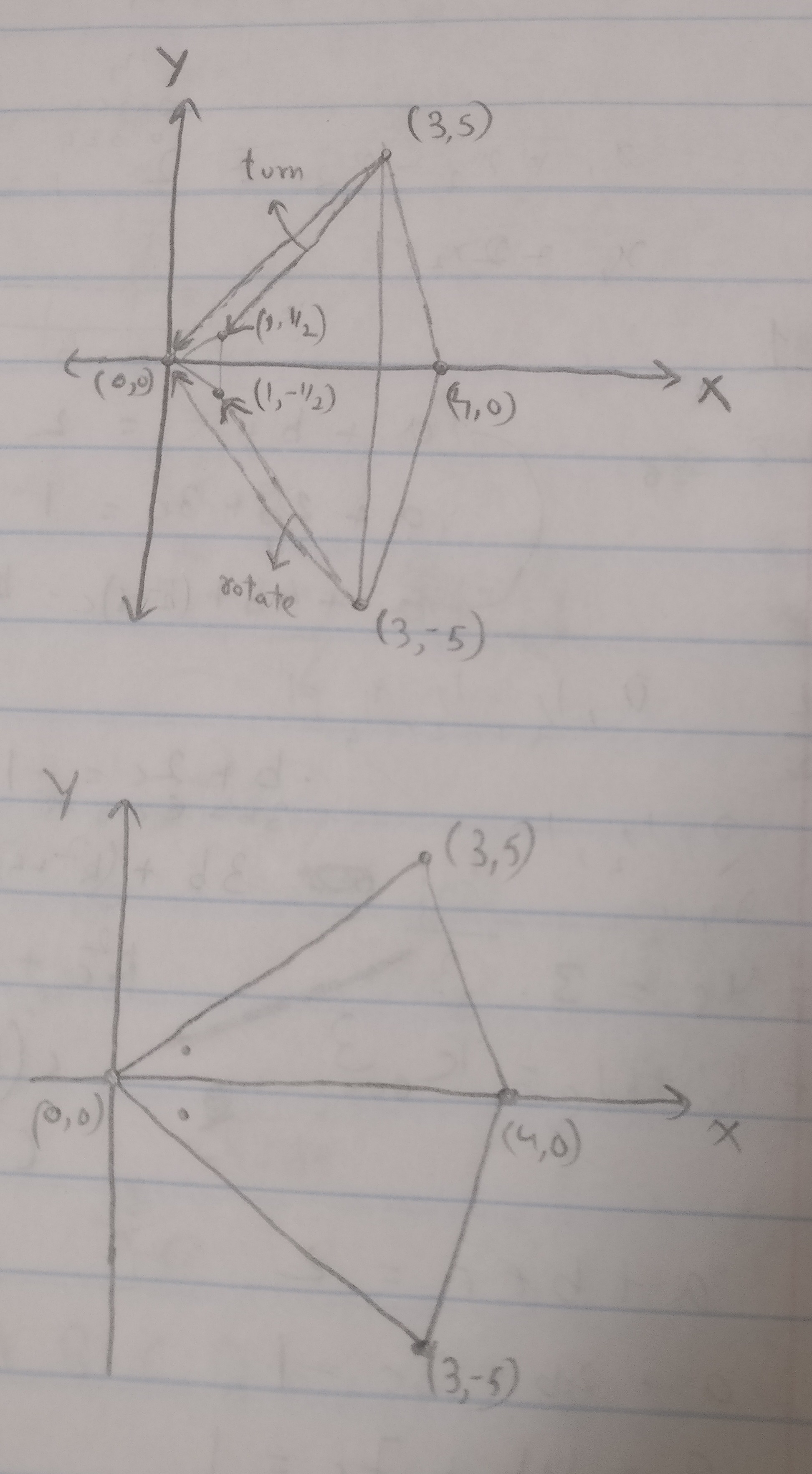
1. We will first the sort the pairs of co-ordinates according to the x-coordinate but in this case they are already in a sorted order.
2. Then we will put the 1st 3 pairs in set 1 and the remaining 3 in set 2.
3. Set 1 = (0,0),(1, 1/2), (1, -1/2) Set 2 = (3, 5), (3, -5), (4, 0)
4. Set 1 forms a small triangle on the left and set 2 forms a bigger triangle on the right.
5. Now we need to connect these 2 triangles, the merging part. For that we will consider (3, 5) and (1, 1/2). The dot product of these 2 is positive and will move in a clockwise direction and connect to (0, 0).
6. Similarly the vector connecting (3, -5) and (1, -1/2) will move outward in an anti-clockwise direction and connect to (0, 0).
The base condition is the individual point itself.
(Edited: 2021-09-27) 1. We will first the sort the pairs of co-ordinates according to the x-coordinate but in this case they are already in a sorted order.
2. Then we will put the 1st 3 pairs in set 1 and the remaining 3 in set 2.
3. Set 1 = (0,0),(1, 1/2), (1, -1/2) Set 2 = (3, 5), (3, -5), (4, 0)
4. Set 1 forms a small triangle on the left and set 2 forms a bigger triangle on the right.
5. Now we need to connect these 2 triangles, the merging part. For that we will consider (3, 5) and (1, 1/2). The dot product of these 2 is positive and will move in a clockwise direction and connect to (0, 0).
6. Similarly the vector connecting (3, -5) and (1, -1/2) will move outward in an anti-clockwise direction and connect to (0, 0).
The base condition is the individual point itself.
- First we need to sort the points based on the x-coordinates
- Divide the set of points into two halves and recursively compute convex hulls
- Merge the results of the divided halves
Base cases
- The base cases here are the single points (The leaf nodes of the below tree).
- The convex hull for a single point is the point itself
Merging
(Edited: 2021-09-27) - For merging, first we connect the y extremes from the left and right convex hulls.
- Then we check if there is a point with lesser x coordinate in the left convex hull. If there is, then we decide to move clockwise based on the cross product of the two vectors(one vector connects points with max y coordinate in the right hull and the point with max y coordinate on the left hull and another vector connects points with max y coordinate in the right hull and the newly found point with lesser x coordinate in the left hull). We move anti-clockwise for smallest y coordinate.
- Similarly, we check if there is a point with greater x coordinate in the right convex hull. If there is, then we decide to move anti-clockwise for max y coordinate vector and clockwise for min y coordinate vector for based on the cross product of the two lines
# First we need to sort the points based on the x-coordinates
# Divide the set of points into two halves and recursively compute convex hulls
# Merge the results of the divided halves
'''Base cases'''
*The base cases here are the single points (The leaf nodes of the below tree).
* The convex hull for a single point is the point itself
'''Merging'''
* For merging, first we connect the y extremes from the left and right convex hulls.
* Then we check if there is a point with lesser x coordinate in the left convex hull. If there is, then we decide to move clockwise based on the cross product of the two vectors(one vector connects points with max y coordinate in the right hull and the point with max y coordinate on the left hull and another vector connects points with max y coordinate in the right hull and the newly found point with lesser x coordinate in the left hull). We move anti-clockwise for smallest y coordinate.
* Similarly, we check if there is a point with greater x coordinate in the right convex hull. If there is, then we decide to move anti-clockwise for max y coordinate vector and clockwise for min y coordinate vector for based on the cross product of the two lines
((resource:New doc Sep 26, 2021 11.24 PM.jpg|Resource Description for New doc Sep 26, 2021 11.24 PM.jpg))
The divide and conquer approach can be used to get the convex hull of this set of points.
1) To begin with, we sort the points by their x-coordinates.
2) Split the set into two halves and call the algorithm recursively on the two sets to compute their convex hulls.
3) Merge the two convex hulls to get the final convex hull.
Merging:
1) Once we get the two convex hulls, we need to find the highest points of those two hulls and connect them.
2) Then we fix the line on the higher point on that line and keep rotate it clockwise while making sure the cross product is positive.
3) Then we repeat the same step as above with the two lowest points of the two hulls, and connect them.
4) Then we fix the line on the lower point on that line and keep rotate it anti-clockwise while making sure the cross product is positive.
The convex hull for a point will be a point, for two points it’s a line, for three points it would be a triangle.
For our problem, the have to find the convex hull for the set of points (0,0),(1,12),(1,−12),(3,5),(3,−5),(4,0).
The points are already sorted by their x-coordinates, so we need to split them in half. We end up with two sets A = {(0,0),(1,12),(1,−12)} and B = {(3,5),(3,−5),(4,0)}. Since they are a set of three points, they form a triangle. Now, we must merge these two triangles.
We take the highest points from the two sets which are (3, 5) and (1, 1/2). We make a line and fix it on the higher point (3, 5). Then we rotate the line clockwise while keeping the cross product positive to the next point which would be the point with the lower x-coordinate in the set A i.e., the point (0, 0). We fix this point as the upper tangent and move on to the lower part.
Now we repeat a similar process with the lower part, we take the lowest points from the two sets which are (3, -5) and (1, -1/2). We make a line and fix it on the lower point (3, -5) and rotate the line anti-clockwise while keeping the cross product positive to the next point in the set A i.e., the point (0, 0). We fix this line as the lower tangent. Our merge is now complete.
Finally, our convex hull for this set would be (0, 0), (3, 5), (3, -5), (4, 0)
(Edited: 2021-09-27) The divide and conquer approach can be used to get the convex hull of this set of points.
1) To begin with, we sort the points by their x-coordinates.
2) Split the set into two halves and call the algorithm recursively on the two sets to compute their convex hulls.
3) Merge the two convex hulls to get the final convex hull.
'''Merging:'''
1) Once we get the two convex hulls, we need to find the highest points of those two hulls and connect them.
2) Then we fix the line on the higher point on that line and keep rotate it clockwise while making sure the cross product is positive.
3) Then we repeat the same step as above with the two lowest points of the two hulls, and connect them.
4) Then we fix the line on the lower point on that line and keep rotate it anti-clockwise while making sure the cross product is positive.
The convex hull for a point will be a point, for two points it’s a line, for three points it would be a triangle.
For our problem, the have to find the convex hull for the set of points (0,0),(1,12),(1,−12),(3,5),(3,−5),(4,0).
The points are already sorted by their x-coordinates, so we need to split them in half. We end up with two sets A = {(0,0),(1,12),(1,−12)} and B = {(3,5),(3,−5),(4,0)}. Since they are a set of three points, they form a triangle. Now, we must merge these two triangles.
We take the highest points from the two sets which are (3, 5) and (1, 1/2). We make a line and fix it on the higher point (3, 5). Then we rotate the line clockwise while keeping the cross product positive to the next point which would be the point with the lower x-coordinate in the set A i.e., the point (0, 0). We fix this point as the upper tangent and move on to the lower part.
Now we repeat a similar process with the lower part, we take the lowest points from the two sets which are (3, -5) and (1, -1/2). We make a line and fix it on the lower point (3, -5) and rotate the line anti-clockwise while keeping the cross product positive to the next point in the set A i.e., the point (0, 0). We fix this line as the lower tangent. Our merge is now complete.
Finally, our convex hull for this set would be (0, 0), (3, 5), (3, -5), (4, 0)
((resource:cs-256 in class excersice sep 22 graph.png|Resource Description for cs-256 in class excersice sep 22 graph.png))
(c) 2026 Yioop - PHP Search Engine