2022-02-16
Feb 16 In-Class Exercise.
Please post your solution to the Feb 16 In-Class Exercise to this thread.
Best,
Chris
Please post your solution to the Feb 16 In-Class Exercise to this thread.
Best,
Chris
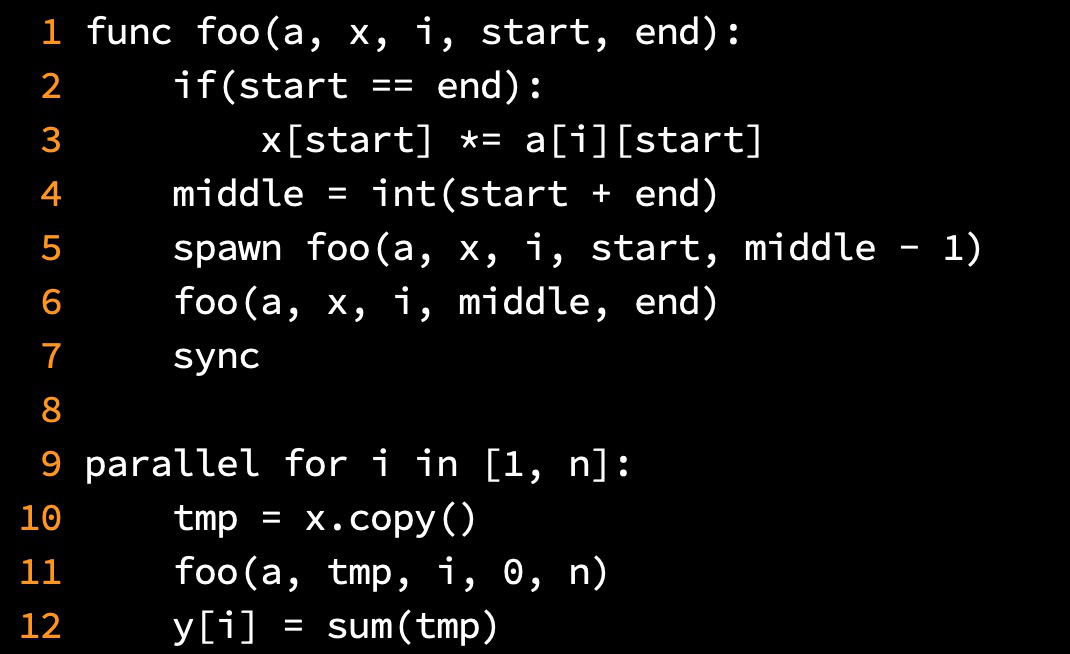
MAT-VEC-MAIN-LOOP-INNER (A, x, y, n, i, j, j') 1 if j == j': 2 return a[i][j] * x[j] 4 else: mid = floor((j + j')/2) 5 n1 = spawn MAT-VEC-MAIN-LOOP-INNER(A, x, y, n, i, j, mid) 6 n2 = MAT-VEC-MAIN-LOOP-INNER(A, x, y, n, i, mid + 1, j') 7 sync 8 return n1+n2 MAT-VEC(A, x) 1 n = A.rows 2 let y be a new vector of length n 3 parallel for i = 1 to n: 4 y[i] = 0 // Setting to 0 is not required 5 parallel for i = 1 to n: 6 y[i] = MAT-VEC-MAIN-LOOP-INNER (A, x, y, n, i, j, j') 8 return y T1 = theta(n^2) Tinf = theta(2logn) T1/Tinf = theta(n^2/2logn) As P is fixed, P << T1/Tinf hence, speedup will not be significant(Edited: 2022-02-20)
<pre>
MAT-VEC-MAIN-LOOP-INNER (A, x, y, n, i, j, j')
1 if j == j':
2 return a[i][j] * x[j]
4 else:
mid = floor((j + j')/2)
5 n1 = spawn MAT-VEC-MAIN-LOOP-INNER(A, x, y, n, i, j, mid)
6 n2 = MAT-VEC-MAIN-LOOP-INNER(A, x, y, n, i, mid + 1, j')
7 sync
8 return n1+n2
MAT-VEC(A, x)
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n:
4 y[i] = 0 // Setting to 0 is not required
5 parallel for i = 1 to n:
6 y[i] = MAT-VEC-MAIN-LOOP-INNER (A, x, y, n, i, j, j')
8 return y
T1 = theta(n^2)
Tinf = theta(2logn)
T1/Tinf = theta(n^2/2logn)
As P is fixed, P << T1/Tinf hence, speedup will not be significant
</pre>
MAT-VEC(A, x) 1 n = A.rows 2 let y be a new vector of length n 3 parallel for i = 1 to n: 4 y[i] = 0 5 parallel for i = 1 to n: 6 y[i] = GET-SUM-PARALLEL(A, x, i, 0, n) 7 return y GET-SUM-PARALLEL (A, x, i, j, j’) 1 if j == j’: 2 return A[I][j] * x[j]; 4 else: 5 mid = floor((j+ j’)/2) 6 first_half_sum = spawn GET-SUM-PARALLEL(A, x, i, j, mid) 7 second_half_sum = GET-SUM-PARALLEL(A, x, I, mid + 1, j') 8 sync 9 return first_half_sum + second_half_sumT1 = theta(n**2) Tinf = theta(log n) T1/Tinf = theta(n**2)/ th(log n) If we have a fixed number of processor, P << T1/Tinf. Hence, we won't get any significant speedup.(Edited: 2022-02-17)
<pre>
MAT-VEC(A, x)
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n:
4 y[i] = 0
5 parallel for i = 1 to n:
6 y[i] = GET-SUM-PARALLEL(A, x, i, 0, n)
7 return y
GET-SUM-PARALLEL (A, x, i, j, j’)
1 if j == j’:
2 return A[I][j] * x[j];
4 else:
5 mid = floor((j+ j’)/2)
6 first_half_sum = spawn GET-SUM-PARALLEL(A, x, i, j, mid)
7 second_half_sum = GET-SUM-PARALLEL(A, x, I, mid + 1, j')
8 sync
9 return first_half_sum + second_half_sum
</pre>
T1 = theta(n**2)
Tinf = theta(log n)
T1/Tinf = theta(n**2)/ th(log n)
If we have a fixed number of processor, P << T1/Tinf. Hence, we won't get any significant speedup.
MAT-VEC(A, x) 1 n = A.rows 2 let y be a new vector of length n 3 parallel for i = 1 to n: 4 y[i] = 0 5 parallel for i = 1 to n: 6 y[i] = spawnSync(A,x,y, i, n, 0 , n-1) 8 return y spawnSync(A,x,y, i, n, j , j') 1 if j == j': 2 return a[i][j] * x[j] 3 else: 4 mid = floor((j+ j')/2) 5 spawn x1 = spawnSync(A, x, y, n, j, mid) 6 x2 = spawnSync(A, x, y, n, mid + 1, j') 7 sync 8 return x1+x2 T_1 = th(n^2) T_inf = th(2 * log n) T_1/T_inf = th( n^2/log n) Since for fixed P, we will have P << T_1/T_inf hence won't help much.(Edited: 2022-02-16)
<pre>
MAT-VEC(A, x)
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n:
4 y[i] = 0
5 parallel for i = 1 to n:
6 y[i] = spawnSync(A,x,y, i, n, 0 , n-1)
8 return y
spawnSync(A,x,y, i, n, j , j')
1 if j == j':
2 return a[i][j] * x[j]
3 else:
4 mid = floor((j+ j')/2)
5 spawn x1 = spawnSync(A, x, y, n, j, mid)
6 x2 = spawnSync(A, x, y, n, mid + 1, j')
7 sync
8 return x1+x2
T_1 = th(n^2)
T_inf = th(2 * log n)
T_1/T_inf = th( n^2/log n)
Since for fixed P, we will have P << T_1/T_inf hence won't help much.
</pre>
MAT-VEC(A, x) n = A.rows let y be a new vector of length n parallel for i = 1 to n: y[i] = 0 parallel for i = 1 to n: L = [] // this will be of size n parallel for j = 1 to n: L[j] = A[i][j]*x[j] return CALCULATE-SUM(L, 0, n-1) CALCULATE-SUM(L, low, high): if low == high: return L[low] N = size(L) mid = floor((low + high)/2) sum1 = spawn CALCULATE-SUM(L, low, mid) sum2 = CALCULATE-SUM(L, mid+1, high) sync return sum1+sum2 Here, Tinf = theta(log n) T1 = theta(n^2) Therefore, parallelism = T1/Tinf = theta(n^2 / logn). We won't get much speedup(Edited: 2022-02-16)
<pre>
MAT-VEC(A, x)
n = A.rows
let y be a new vector of length n
parallel for i = 1 to n:
y[i] = 0
parallel for i = 1 to n:
L = [] // this will be of size n
parallel for j = 1 to n:
L[j] = A[i][j]*x[j]
return CALCULATE-SUM(L, 0, n-1)
CALCULATE-SUM(L, low, high):
if low == high:
return L[low]
N = size(L)
mid = floor((low + high)/2)
sum1 = spawn CALCULATE-SUM(L, low, mid)
sum2 = CALCULATE-SUM(L, mid+1, high)
sync
return sum1+sum2
Here, Tinf = theta(log n)
T1 = theta(n^2)
Therefore, parallelism = T1/Tinf = theta(n^2 / logn).
We won't get much speedup
</pre>
The following rewrite of the algorithm MAT-VEC (and the helper functions) uses spawn/sync to parallelize the loops, including the inner for loop on j:
MAT-VEC(A, x):
n = A.rows let y be a new vector of length n MAT-VEC-FIRST-LOOP(y, 1, n) MAT-VEC-SECOND-LOOP(A, x, y, n, 1, n) return y
MAT-VEC-FIRST-LOOP(y, i, i'):
if i == i': y[i] = 0 else: mid = floor((i + i')/2) first = spawn MAT-VEC-FIRST-LOOP(y, i, mid) second = MAT-VEC-FIRST-LOOP(y, mid + 1, i') sync return first + second
MAT-VEC-SECOND-LOOP(A, x, y, n, i, i'):
if i == i': MAT-VEC-THIRD-LOOP(A, x, y, i, 1, n) else: mid = floor((i + i')/2) spawn MAT-VEC-SECOND-LOOP(A, x, y, n, i, mid) MAT-VEC-SECOND-LOOP(A, x, y, n, mid + 1, i') sync
MAT-VEC-THIRD-LOOP(A, x, y, i, j, j'):
if j == j': y[i] = y[i] + a[i][j] * x[j] else: mid = floor((j + j')/2) first = spawn MAT-VEC-THIRD-LOOP(A, x, y, i, j, mid) second = MAT-VEC-THIRD-LOOP(A, x, y, i, mid + 1, j') sync return first + second
T_1 = theta(n^2) since we have doubly nested loops
span(MAT-VEC-FIRST-LOOP) = theta(log n) since each iteration is theta(1)
span(MAT-VEC-THIRD-LOOP) = theta(log n) since each iteration is theta(1)
span(MAT-VEC-SECOND-LOOP) = theta(log n + log n) = theta(2 log n) since each iteration is theta(log n)
T_inf = theta(log n) + max(span(MAT-VEC-FIRST-LOOP)) + theta(log n) + max(span(MAT-VEC-SECOND-LOOP)) = theta(log n) + theta(log n) + theta(log n) + theta(2 log n) = theta(log n) dominates
T_1/T_inf = theta(n^2)/theta(log n) = theta(n^2/(log n))
The added complexity is not worth it since the parallelism grows exponentially, indicating that given a large fixed number of processors, the algorithm will exhibit nearly perfect linear speedup which is not significant enough at larger values.
(Edited: 2022-02-16) The following rewrite of the algorithm MAT-VEC (and the helper functions) uses spawn/sync to parallelize the loops, including the inner for loop on j:
MAT-VEC(A, x):
n = A.rows
let y be a new vector of length n
MAT-VEC-FIRST-LOOP(y, 1, n)
MAT-VEC-SECOND-LOOP(A, x, y, n, 1, n)
return y
MAT-VEC-FIRST-LOOP(y, i, i'):
if i == i':
y[i] = 0
else:
mid = floor((i + i')/2)
first = spawn MAT-VEC-FIRST-LOOP(y, i, mid)
second = MAT-VEC-FIRST-LOOP(y, mid + 1, i')
sync
return first + second
MAT-VEC-SECOND-LOOP(A, x, y, n, i, i'):
if i == i':
MAT-VEC-THIRD-LOOP(A, x, y, i, 1, n)
else:
mid = floor((i + i')/2)
spawn MAT-VEC-SECOND-LOOP(A, x, y, n, i, mid)
MAT-VEC-SECOND-LOOP(A, x, y, n, mid + 1, i')
sync
MAT-VEC-THIRD-LOOP(A, x, y, i, j, j'):
if j == j':
y[i] = y[i] + a[i][j] * x[j]
else:
mid = floor((j + j')/2)
first = spawn MAT-VEC-THIRD-LOOP(A, x, y, i, j, mid)
second = MAT-VEC-THIRD-LOOP(A, x, y, i, mid + 1, j')
sync
return first + second
T_1 = theta(n^2) since we have doubly nested loops
span(MAT-VEC-FIRST-LOOP) = theta(log n) since each iteration is theta(1)
span(MAT-VEC-THIRD-LOOP) = theta(log n) since each iteration is theta(1)
span(MAT-VEC-SECOND-LOOP) = theta(log n + log n) = theta(2 log n) since each iteration is theta(log n)
T_inf = theta(log n) + max(span(MAT-VEC-FIRST-LOOP)) + theta(log n) + max(span(MAT-VEC-SECOND-LOOP)) = theta(log n) + theta(log n) + theta(log n) + theta(2 log n) = theta(log n) dominates
T_1/T_inf = theta(n^2)/theta(log n) = theta(n^2/(log n))
The added complexity is not worth it since the parallelism grows exponentially, indicating that given a large fixed number of processors, the algorithm will exhibit nearly perfect linear speedup which is not significant enough at larger values.
T_1/T_inf = theta(n^2 / logn).
(Edited: 2022-03-12) We won't get much speedup
((resource:Screen Shot 2022-02-16 at 5.34.27 PM.jpg|Resource Description for Screen Shot 2022-02-16 at 5.34.27 PM.jpg))
T_1/T_inf = theta(n^2 / logn).
We won't get much speedup
n = A.rows
let y be a new vector of length n
parallel for i = 1 to n:
(Edited: 2022-02-16)
y[i] = 0
x = []
spawn i:n processes:
y[n] = spawn all(y[n] + a[n][n] * x[n]
x.append(all spawned y[n])
if all spawns compute:
sync(x.values)
return y
n = A.rows
let y be a new vector of length n
parallel for i = 1 to n:
y[i] = 0
x = []
spawn i:n processes:
y[n] = spawn all(y[n] + a[n][n] * x[n]
x.append(all spawned y[n])
if all spawns compute:
sync(x.values)
return y
MAT-VEC(A, x) 1 n = A.rows 2 let y be a new vector of length n 3 parallel for i = 1 to n: 4 y[i] = 0 5 parallel for i = 1 to n: 6 y[i] = MAT_VEC_INNER_LOOP(A,x,y,n,j,j') 8 return y 9 function MAT_VEC_INNER_LOOP(A,x,y,n,j,j') 10 if j=j': 11 return a[i][j] * x[j]; 12 else 13 mid=((j+j')/2); 14 var1 = spawn MAT-VEC-MAIN-LOOP(A, x, y, n, j, mid) 15 var2 = MAT-VEC-MAIN-LOOP(A, x, y, n, mid + 1, j') 16 sync 17. return var1+var2;
T1 = O(n^2) Tinf = O (logn) Parallelism= T1/Tinf= O(n^2)/O(logn) which makes it an undesirable option as compared to the parallel algorithm discussed in class.(Edited: 2022-02-17)
<pre>
MAT-VEC(A, x)
1 n = A.rows
2 let y be a new vector of length n
3 parallel for i = 1 to n:
4 y[i] = 0
5 parallel for i = 1 to n:
6 y[i] = MAT_VEC_INNER_LOOP(A,x,y,n,j,j')
8 return y
9 function MAT_VEC_INNER_LOOP(A,x,y,n,j,j')
10 if j=j':
11 return a[i][j] * x[j];
12 else
13 mid=((j+j')/2);
14 var1 = spawn MAT-VEC-MAIN-LOOP(A, x, y, n, j, mid)
15 var2 = MAT-VEC-MAIN-LOOP(A, x, y, n, mid + 1, j')
16 sync
17. return var1+var2;
</pre>
T1 = O(n^2)
Tinf = O (logn)
Parallelism= T1/Tinf= O(n^2)/O(logn) which makes it an undesirable option as compared to the parallel algorithm discussed in class.
MAT-VEC(A, x) n = A.rows let y be a new vector of length n parallel for i = 1 to n: y[i] = 0 parallel for i = 1 to n: y[i] = innerloop(A, x, y, n, j, j') return y innerloop(A, x, y, n, j, j') if j = j': return a[i][j]*y[j] else: mid = floor((j+j')/2) spawn x = innerloop(A, x, y, n, j, mid) x' = innerloop(A, x, y, n, mid+1, j') sync return (x+x')
Here, Tinf = theta(log n)
T1 = theta(n^2)
(Edited: 2022-02-17) Therefore, parallelism = T1/Tinf = theta(n^2 / logn).
We won't get much speedup
<pre>
MAT-VEC(A, x)
n = A.rows
let y be a new vector of length n
parallel for i = 1 to n:
y[i] = 0
parallel for i = 1 to n:
y[i] = innerloop(A, x, y, n, j, j')
return y
innerloop(A, x, y, n, j, j')
if j = j':
return a[i][j]*y[j]
else:
mid = floor((j+j')/2)
spawn x = innerloop(A, x, y, n, j, mid)
x' = innerloop(A, x, y, n, mid+1, j')
sync
return (x+x')
</pre>
Here, Tinf = theta(log n)
T1 = theta(n^2)
Therefore, parallelism = T1/Tinf = theta(n^2 / logn).
We won't get much speedup
(c) 2025 Yioop - PHP Search Engine