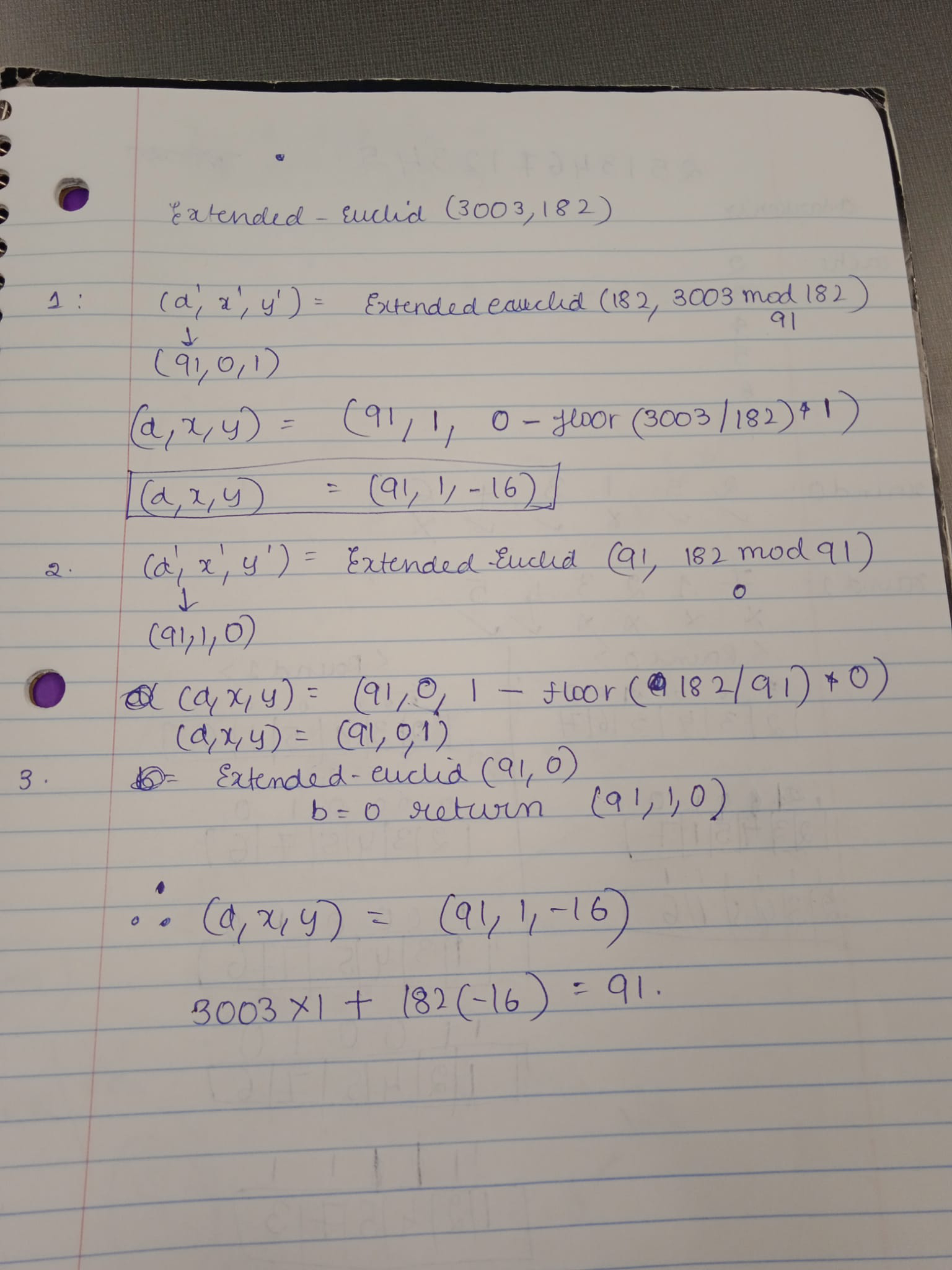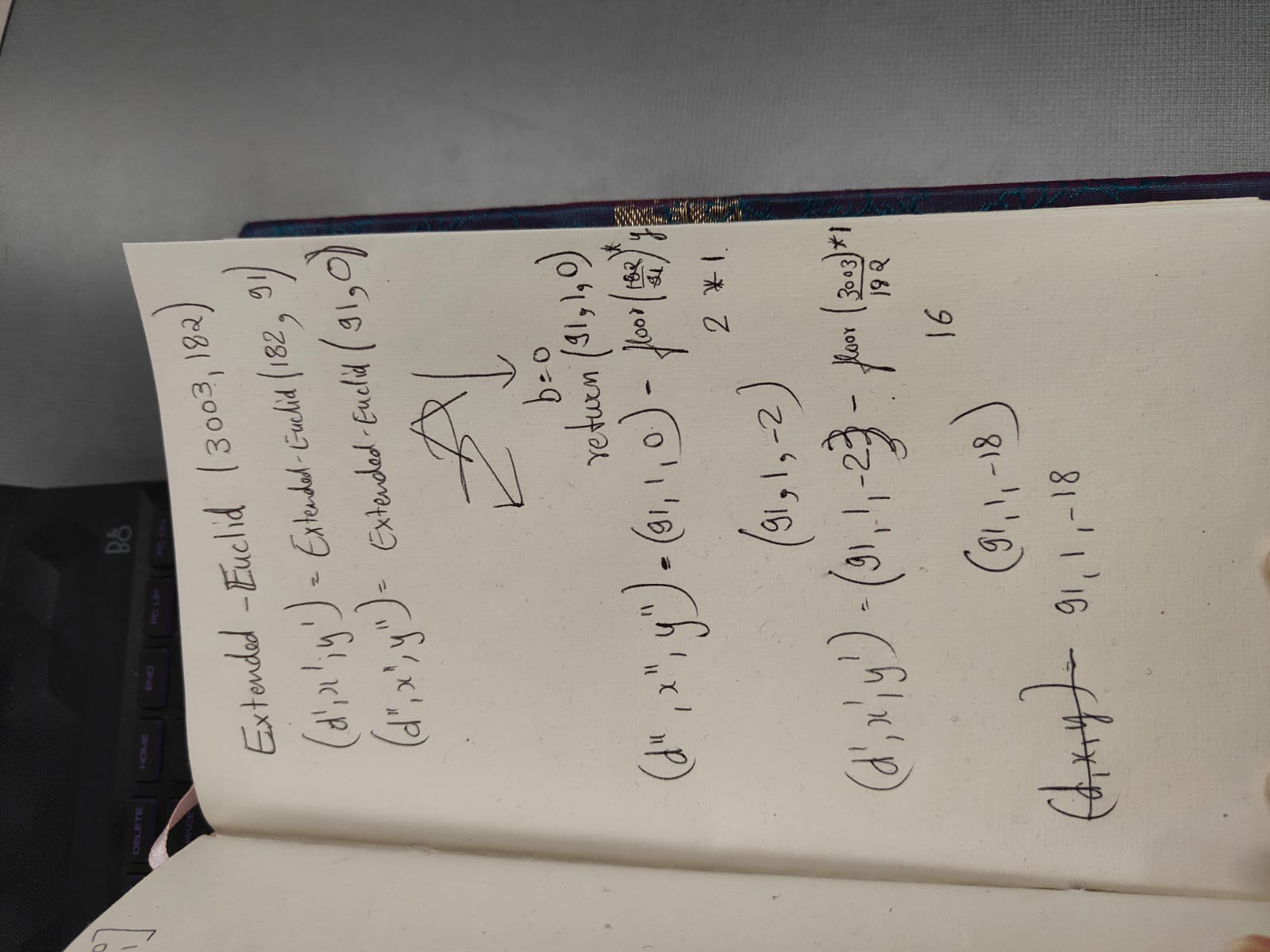Yioop - PHP Search Engine

Apr 6 In-Class Exercise Thread.

Please post your solutions to the Apr 6 In-Class Exercise to this thread.

Best,

Chris

Please post your solutions to the Apr 6 In-Class Exercise to this thread. Best, Chris

-- Apr 6 In-Class Exercise Thread

Outer

1. call Extended-Euclid(3003, 182)

2. check b != 0

3. calculate a mod b = 3003 mod 182 = 91

4. (d', x', y') = Extended-Euclid(182, 91)

Inner 1

5. call Extended-Euclid(182, 91)

6. check b != 0

7. calculate a mod b = 182 mod 91 = 0

8. (d', x', y') = Extended-Euclid(91, 0)

Inner 2

9. call Extended-Euclid(91, 0)

10. check b = 0, return (91, 1, 0)

Inner 1

11. calculate x' - floor(a/b) * y' = 1 - floor(182/91) * 0 = 1

12. (d, x, y) = (91, 0, 1)

13. return (91, 0, 1)

Outer

14. calculate x' - floor(a/b) * y' = 0 - floor(3003/182) * 1 = -16

15. (d, x, y) = (91, 1, -16)

16. return (91, 1, -16)

Verification

3003 * 1 + 182 * -16 = 91 = d = gcd(3003, 182)

(Edited: 2022-04-06)

Outer 1. call Extended-Euclid(3003, 182) 2. check b != 0 3. calculate a mod b = 3003 mod 182 = 91 4. (d', x', y') = Extended-Euclid(182, 91) Inner 1 5. call Extended-Euclid(182, 91) 6. check b != 0 7. calculate a mod b = 182 mod 91 = 0 8. (d', x', y') = Extended-Euclid(91, 0) Inner 2 9. call Extended-Euclid(91, 0) 10. check b = 0, return (91, 1, 0) Inner 1 11. calculate x' - floor(a/b) * y' = 1 - floor(182/91) * 0 = 1 12. (d, x, y) = (91, 0, 1) 13. return (91, 0, 1) Outer 14. calculate x' - floor(a/b) * y' = 0 - floor(3003/182) * 1 = -16 15. (d, x, y) = (91, 1, -16) 16. return (91, 1, -16) Verification 3003 * 1 + 182 * -16 = 91 = d = gcd(3003, 182)

-- Apr 6 In-Class Exercise Thread

Extended-Euclid(3003,182)
{
	b!=0
	(d', x', y') = Extended-Euclid(182, 91)
	{
		b != 0
		(d', x', y') = Extended-Euclid(91, 0)
		{
			b = 0, return (91, 1, 0)
		}
		(d, x, y) = (91, 0, 1 - floor(182/91) * 0)
			= (91, 0, 1)
		return (91, 0, 1)
	}
	(d, x, y) = (91, 1, 0 - floor(3003/182) * 1)
		= (91, 1, -16)
	return (91, 1, -16)

} (Edited: 2022-04-06)

<pre> Extended-Euclid(3003,182) { b!=0 (d', x', y') = Extended-Euclid(182, 91) { b != 0 (d', x', y') = Extended-Euclid(91, 0) { b = 0, return (91, 1, 0) } (d, x, y) = (91, 0, 1 - floor(182/91) * 0) = (91, 0, 1) return (91, 0, 1) } (d, x, y) = (91, 1, 0 - floor(3003/182) * 1) = (91, 1, -16) return (91, 1, -16) } </pre>

-- Apr 6 In-Class Exercise Thread

EE(3003, 182)
    d'x'y' = EE(182, 91)
    dxy = (d',y',x' - 16*y')
    return dxy 
 
 EE(182, 91)
    d'x'y' = EE(91, 0)
    dxy = (d',y',x' - 2*y')
    return dxy 
 
 EE(91, 0)
    return 91, 1, 0 
 
 EE(182, 91)
    d'x'y' =91, 1, 0
    dxy = (91,0,1)
    return (91,0,1) 
 
EE(3003, 182)
    d'x'y' = (91,0,1)
    dxy = (91, 1, -16)
    return (91, 1, -16)

<pre> EE(3003, 182) d'x'y' = EE(182, 91) dxy = (d',y',x' - 16*y') return dxy EE(182, 91) d'x'y' = EE(91, 0) dxy = (d',y',x' - 2*y') return dxy EE(91, 0) return 91, 1, 0 EE(182, 91) d'x'y' =91, 1, 0 dxy = (91,0,1) return (91,0,1) EE(3003, 182) d'x'y' = (91,0,1) dxy = (91, 1, -16) return (91, 1, -16) </pre>

-- Apr 6 In-Class Exercise Thread

((resource:WhatsApp Image 2022-04-06 at 5.36.55 PM.jpeg|Resource Description for WhatsApp Image 2022-04-06 at 5.36.55 PM.jpeg))

-- Apr 6 In-Class Exercise Thread

((resource:WhatsApp Image 2022-04-06 at 5.34.19 PM.jpg|Resource Description for WhatsApp Image 2022-04-06 at 5.34.19 PM.jpg))

-- Apr 6 In-Class Exercise Thread

((resource:WhatsApp Image 2022-04-06 at 5.36.44 PM.jpeg|Resource Description for WhatsApp Image 2022-04-06 at 5.36.44 PM.jpeg))

-- Apr 6 In-Class Exercise Thread

Extended-Euclid(3003, 182)
3003 mod 182 = 91
so 
(d', x', y') = Extended-Euclid(182, 91)
					182 mod 91 = 0
					(d', x', y') = Extended-Euclid(91, 0)
										return (91, 1, 0)
					(d', x', y') = (91, 1, 0)
					(d, x, y) = (91, 0, 1 - 2*0)
					(d, x, y) = (91, 0, 1)
					return (91, 0, 1)

(d', x', y') = (91, 0, 1) (d, x, y) = (91, 1, 0 - 16*1) return (91, 1, -16)

For ax + by = d we have:
(3003)(1) + (182)(-16) = 91 
  
gcd(3003,182) = 91

(Edited: 2022-04-06)

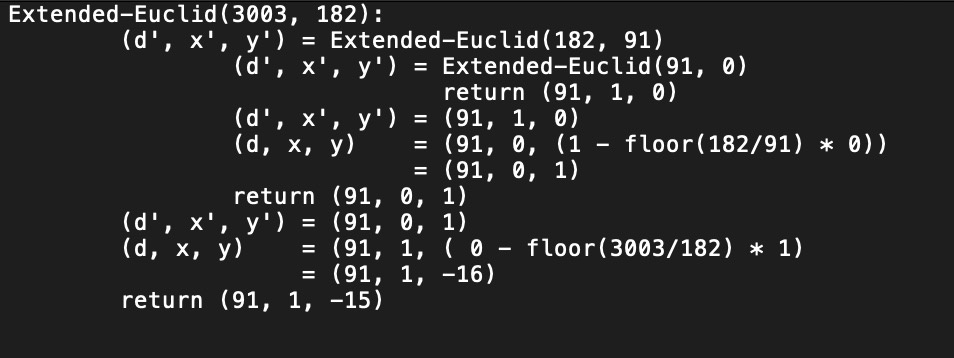
<pre> Extended-Euclid(3003, 182) 3003 mod 182 = 91 so (d', x', y') = Extended-Euclid(182, 91) 182 mod 91 = 0 (d', x', y') = Extended-Euclid(91, 0) return (91, 1, 0) (d', x', y') = (91, 1, 0) (d, x, y) = (91, 0, 1 - 2*0) (d, x, y) = (91, 0, 1) return (91, 0, 1) (d', x', y') = (91, 0, 1) (d, x, y) = (91, 1, 0 - 16*1) return (91, 1, -16) </pre> <pre> For ax + by = d we have: (3003)(1) + (182)(-16) = 91 gcd(3003,182) = 91 </pre>

-- Apr 6 In-Class Exercise Thread

Calculate Extended Euclid(3003, 182)
b = 182, not 0
(d’, x’, y’) = Extended Euclid(182, 3003 mod 182) = Extended Euclid(182, 91) 
 
Calculate Extended Euclid(182, 91)
b = 91, not 0
(d’, x’, y’) = Extended Euclid(91, 182 mod 91) = Extended Euclid(91, 0) 
 
Calculate Extended Euclid(91, 0)
Since b = 0,
return (91, 1, 0) 
 
Back to Extended Euclid(182, 91)
(d’, x’, y’) = Extended Euclid(91, 0) = (91, 1, 0)
(d, x, y) = (91, 0, 1 - floor(182/91)*0)
return (91, 0, 1) 
 
Back to Euclid(3003, 182)
(d’, x’, y’) = Extended Euclid(182, 91) = (91, 0, 1)
(d, x, y) = (91, 1, 0 - floor(3003/182)*1)
return (91, 1, -16) 
 
For ax + by = d,
(3003)(1) + (182)(-16) = 91 
 
So gcd(3003, 182) = 91

<pre> Calculate Extended Euclid(3003, 182) b = 182, not 0 (d’, x’, y’) = Extended Euclid(182, 3003 mod 182) = Extended Euclid(182, 91) Calculate Extended Euclid(182, 91) b = 91, not 0 (d’, x’, y’) = Extended Euclid(91, 182 mod 91) = Extended Euclid(91, 0) Calculate Extended Euclid(91, 0) Since b = 0, return (91, 1, 0) Back to Extended Euclid(182, 91) (d’, x’, y’) = Extended Euclid(91, 0) = (91, 1, 0) (d, x, y) = (91, 0, 1 - floor(182/91)*0) return (91, 0, 1) Back to Euclid(3003, 182) (d’, x’, y’) = Extended Euclid(182, 91) = (91, 0, 1) (d, x, y) = (91, 1, 0 - floor(3003/182)*1) return (91, 1, -16) For ax + by = d, (3003)(1) + (182)(-16) = 91 So gcd(3003, 182) = 91 </pre>

-- Apr 6 In-Class Exercise Thread

((resource:Screen Shot 2022-04-06 at 5.41.00 PM.jpg|Resource Description for Screen Shot 2022-04-06 at 5.41.00 PM.jpg))