2019-02-26
Feb 27 In-Class Exercise Thread .
Post your solutions to the Feb 27 In-Class Exercise to this thread
Best,
Chris
Post your solutions to the Feb 27 In-Class Exercise to this thread
Best,
Chris
How many different types sorting subroutines does BoxSort involve?
``
Solution:
- Pick `\sqrt{n}` elements and sort them to be "splitters"
-
Insert the remaining elements between the splitters using binary search. (a rough, partial sort. not a full sort) - Recurse with BoxSort on subproblems greater than size `\log n`
- Otherwise, use LogSort
Therefore there are three different types sorting subroutines involved in BoxSort (including BoxSort itself!).
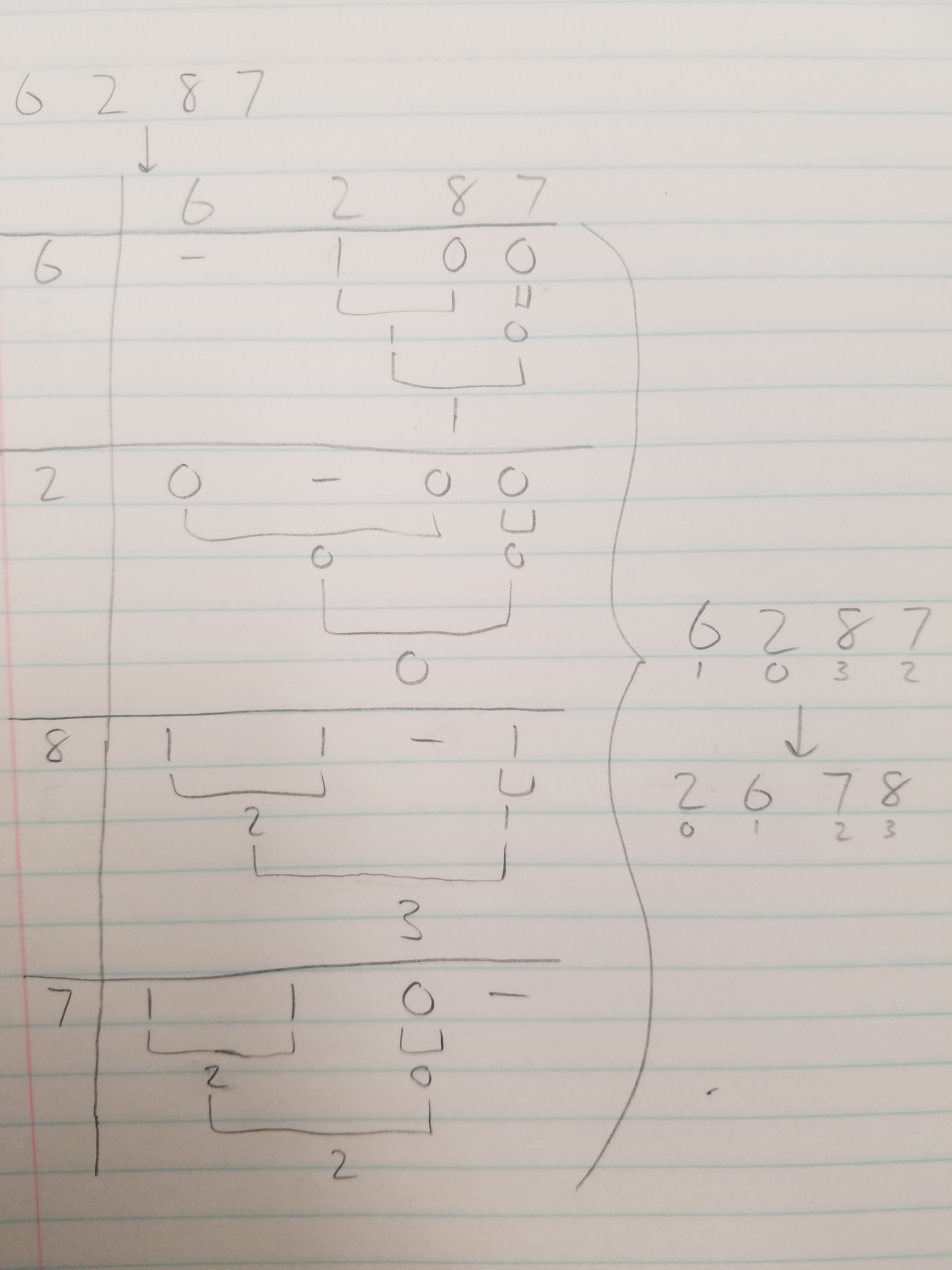
For the first of the subtype used to sort `\sqrt{n}` splitter elements, show how would it sort 6,2,8,7? (Show step by step.)
``
Solution: From slides, "To do the sorting we imagine for each `i` of the `\sqrt{n}` many elements of `R`, using `sqrt{n}−1` processors to compare it with the other `\sqrt{n}−1` elements, then using `O(\log n)` time to sum the values of these comparisons to determine the number of elements smaller than `i`."
``
Use 3 processors for each element `i\in\{6, 2, 8, 7\}` to compare to the other elements. A total of 12 processors assign the following values, where each '1' represents being greater than some other element `j\in\{6, 2, 8, 7\}` where `j != i`. We sum the results from all the processors using a `\log`-sized tree in `O(\log n)` time.
- 6 - 1
- 2 - 0
- 8 - 3
- 7 - 2
Therefore, the sorted order, corresponding to `\{0, 1, 2, 3\}` for the values returned by summing the comparisons from each processor, is `\{2, 6, 7, 8\}`. We use the result of as the array index to place the corresponding splitter.
(Edited: 2019-02-27) ''How many different types sorting subroutines does BoxSort involve?''
@BT@@BT@
'''Solution:'''
# Pick @BT@\sqrt{n}@BT@ elements and sort them to be "splitters"
# <s>Insert the remaining elements between the splitters using binary search. (a rough, partial sort. not a full sort)</s>
# Recurse with BoxSort on subproblems greater than size @BT@\log n@BT@
# Otherwise, use LogSort
Therefore there are '''three''' different types sorting subroutines involved in BoxSort (including BoxSort itself!).
----
''For the first of the subtype used to sort @BT@\sqrt{n}@BT@ splitter elements, show how would it sort 6,2,8,7? (Show step by step.)
''
@BT@@BT@
'''Solution:''' From slides, "To do the sorting we imagine for each @BT@i@BT@ of the @BT@\sqrt{n}@BT@ many elements of @BT@R@BT@, using @BT@sqrt{n}−1@BT@ processors to compare it with the other @BT@\sqrt{n}−1@BT@ elements, then using @BT@O(\log n)@BT@ time to sum the values of these comparisons to determine the number of elements smaller than @BT@i@BT@."
@BT@@BT@
Use 3 processors for each element @BT@i\in\{6, 2, 8, 7\}@BT@ to compare to the other elements. A total of 12 processors assign the following values, where each '1' represents being greater than some other element @BT@j\in\{6, 2, 8, 7\}@BT@ where @BT@j != i@BT@. We sum the results from all the processors using a @BT@\log@BT@-sized tree in @BT@O(\log n)@BT@ time.
* 6 - 1
* 2 - 0
* 8 - 3
* 7 - 2
Therefore, the sorted order, corresponding to @BT@\{0, 1, 2, 3\}@BT@ for the values returned by summing the comparisons from each processor, is @BT@\{2, 6, 7, 8\}@BT@. We use the result of as the array index to place the corresponding splitter.
1. There are three types of sorting subroutines. 2. For 6, 2, 8, 7, use three processors to compare and count numbers less than the current number. 6 Processor 1 compares 6 and 2 and outputs 1 since 2 < 6. Processor 2 compares 6 and 8 and outputs 0. Processor 3 compares 6 and 7 and outputs 0. The result is [1 0 0]. The sum is calculated in parallel in three (log n) operations. p1 + p2 = 1, p3 = 0, 1 + 0 = 1 The sum of these outputs is 1 so 6 goes in position 1.
2 goes into position 0 since [0 0 0] sums up to 0. 8 goes into position 3 since [1 1 1] sums up to 3. 7 goes into position 2 since [1 0 1] sums up to 2.
The result is [2, 6, 7, 8](Edited: 2019-02-27)
1. There are three types of sorting subroutines.
2. For 6, 2, 8, 7, use three processors to compare and count numbers less than the current number.
6
Processor 1 compares 6 and 2 and outputs 1 since 2 < 6.
Processor 2 compares 6 and 8 and outputs 0.
Processor 3 compares 6 and 7 and outputs 0.
The result is [1 0 0].
The sum is calculated in parallel in three (log n) operations. p1 + p2 = 1, p3 = 0, 1 + 0 = 1
The sum of these outputs is 1 so 6 goes in position 1.
2 goes into position 0 since [0 0 0] sums up to 0.
8 goes into position 3 since [1 1 1] sums up to 3.
7 goes into position 2 since [1 0 1] sums up to 2.
The result is [2, 6, 7, 8]
1. There are 3 subroutines within BoxSort, namely logSort, Binary Search and Recursive BoxSort.
2. To sort 6,2,8,7. Pick X^(1/2) = 4 so X = 16.
Splitters randomly: say 6,2. and sort 6,2 to 2,6.
Then use the 4^(1/2) - 1 = 3 to compare with already sorted [2,6]
(Edited: 2019-03-04) 1. compare 6 to 2, 8,7 => [ 0 0 1] => 1 2. compare 2 to 6 8 7 => [0 0 0] => 0 3. compare 8 to 6 2 7 => [1 1 1] => 3 4. compare 7 to 6 2 8 => [0 1 1] => 2
1. There are 3 subroutines within BoxSort, namely logSort, Binary Search and Recursive BoxSort.
2. To sort 6,2,8,7. Pick X^(1/2) = 4 so X = 16.
Splitters randomly: say 6,2. and sort 6,2 to 2,6.
Then use the 4^(1/2) - 1 = 3 to compare with already sorted [2,6]
1. compare 6 to 2, 8,7 => [ 0 0 1] => 1
2. compare 2 to 6 8 7 => [0 0 0] => 0
3. compare 8 to 6 2 7 => [1 1 1] => 3
4. compare 7 to 6 2 8 => [0 1 1] => 2
How many different types sorting subroutines does BoxSort involve?
Ans. 3 types
For the first of the subtypes used to sort √n splitter elements, show how would it sort 6,2,8,7? (Show step by step.)
Use sqrt(n)-1 = 3 processors for element i∈{6,2,8,7}.
We assign '1' when element is greater than some other element j∈{6,2,8,7} and then accumulate. 12 processors assign the following values and we get 6 - 1, 2 - 0, 8 - 3, 7 - 2
Hence, sorted order, is {2,6,7,8}.
How many different types sorting subroutines does BoxSort involve?
Ans. 3 types
For the first of the subtypes used to sort √n splitter elements, show how would it sort 6,2,8,7? (Show step by step.)
Use sqrt(n)-1 = 3 processors for element i∈{6,2,8,7}.
We assign '1' when element is greater than some other element j∈{6,2,8,7} and then accumulate. 12 processors assign the following values and we get 6 - 1, 2 - 0, 8 - 3, 7 - 2
Hence, sorted order, is {2,6,7,8}.
1. 3 types of subroutines: binary search, logSort, sqrt(n) indices sorting similar with QuickSort
2. sqrt(n=16) = 4 i.e. [ 6 2 8 7 ]
for i=6, compare 6 to 2, 8,7 => [1 0 0 ]
for i=2, compare 2 to 6 8 7 => [0 0 0]
for i=8, compare 8 to 6 2 7 => [1 1 1]
for i=7, compare 7 to 6 2 8 => [1 1 0]
summation of each array/sector elements is [1 0 3 2], which serves as indices in the ascending sorted array of splitters
therefore sorted splitters is [2 6 7 8].
(Edited: 2019-02-27) 1. 3 types of subroutines: binary search, logSort, sqrt(n) indices sorting similar with QuickSort
2. sqrt(n=16) = 4 i.e. [ 6 2 8 7 ]
for i=6, compare 6 to 2, 8,7 => [1 0 0 ]
for i=2, compare 2 to 6 8 7 => [0 0 0]
for i=8, compare 8 to 6 2 7 => [1 1 1]
for i=7, compare 7 to 6 2 8 => [1 1 0]
summation of each array/sector elements is [1 0 3 2], which serves as indices in the ascending sorted array of splitters
therefore sorted splitters is [2 6 7 8].
There are three types of sorting subroutines: sorting the splitters,
recursing with BoxSort, and using LogSort.
Sorting the splitters:
Initial order of splitters: 6,2,8,7
Number of splitters is sqrt(n)
4 = sqrt(n), n = 16
Use sqrt(n) - 1 = 3 processors to compare each splitter with the other 3 splitters
Record and sum in O(log n) time the number of times splitter is larger than other splitters.
6: 1, larger than 2
2: 0
8: 3, larger than 6,2,7
7: 2, larger than 6,2
Use these as the new indices for the array of splitters
[2,6,7,8]
(Edited: 2019-02-27) There are three types of sorting subroutines: sorting the splitters,
recursing with BoxSort, and using LogSort.
Sorting the splitters:
Initial order of splitters: 6,2,8,7
Number of splitters is sqrt(n)
4 = sqrt(n), n = 16
Use sqrt(n) - 1 = 3 processors to compare each splitter with the other 3 splitters
Record and sum in O(log n) time the number of times splitter is larger than other splitters.
6: 1, larger than 2
2: 0
8: 3, larger than 6,2,7
7: 2, larger than 6,2
Use these as the new indices for the array of splitters
[2,6,7,8]
1. There are 3 types of sorting in the BoxSort algorithm:
type 1: We compare the sqrt(n) -1 element to other sqrt(n) - 1 element of R using the sum of the comparisons
type 2: We do a logSort by comparing adjacent elements.
type 3: The overall algorithm
2. With our splitters as <6, 2, 8, 7> we create an array of size sqrt(n) that contains the splitters in the order that they appear in the original array.
Using sqrt(n) - 1 many processors (3) we compare the splitter to the other splitters and that outputs a bit b_i that indiciates 0 if the splitter is smaller and 1 if the splitter is larger. We then sum the b_i to get the resulting position of the splitter. The positions of the splitters are then swapped to the corresponding positions of the previous splitter locations.
6 - {1, 0, 0} = 1
2 - {0, 0, 0} = 0
8 - {1, 1, 1} = 3
7 - {1, 1, 0} = 2
resulting new indicies: [2, 6, 7, 8]
We then recurse on each of the inbetween elements of each splitter.
(Edited: 2019-02-27) 1. There are 3 types of sorting in the BoxSort algorithm:
type 1: We compare the sqrt(n) -1 element to other sqrt(n) - 1 element of R using the sum of the comparisons
type 2: We do a logSort by comparing adjacent elements.
type 3: The overall algorithm
2. With our splitters as <6, 2, 8, 7> we create an array of size sqrt(n) that contains the splitters in the order that they appear in the original array.
Using sqrt(n) - 1 many processors (3) we compare the splitter to the other splitters and that outputs a bit b_i that indiciates 0 if the splitter is smaller and 1 if the splitter is larger. We then sum the b_i to get the resulting position of the splitter. The positions of the splitters are then swapped to the corresponding positions of the previous splitter locations.
6 - {1, 0, 0} = 1
2 - {0, 0, 0} = 0
8 - {1, 1, 1} = 3
7 - {1, 1, 0} = 2
resulting new indicies: [2, 6, 7, 8]
We then recurse on each of the inbetween elements of each splitter.
1. One sorting subroutine involves sorting the n^.5 randomly chosen array R. For elements inserted on the chosen splitter index, perform the BoxSort on those elements if the size of the inserted elements exceed log(n). Otherwise use LogSort. In total, there are three subroutines: the BoxSort, the LogSort, and the sorting done in the first part of BoxSort for array R.
2. For the array 6,2,8,7:
For each element in the array, compare the element to the other elements and output 0 if the element is less than the compared element and 1 otherwise. Then for each element, sum the outputs.
Once the comparisons are done, the sums are:
6-1
2-0
8-3
7-2
The sum of the element determines the position of the array. Thus the sorted array would be:
2,6,7,8
1. One sorting subroutine involves sorting the n^.5 randomly chosen array R. For elements inserted on the chosen splitter index, perform the BoxSort on those elements if the size of the inserted elements exceed log(n). Otherwise use LogSort. In total, there are three subroutines: the BoxSort, the LogSort, and the sorting done in the first part of BoxSort for array R.
2. For the array 6,2,8,7:
For each element in the array, compare the element to the other elements and output 0 if the element is less than the compared element and 1 otherwise. Then for each element, sum the outputs.
Once the comparisons are done, the sums are:
6-1
2-0
8-3
7-2
The sum of the element determines the position of the array. Thus the sorted array would be:
2,6,7,8
(c) 2026 Yioop - PHP Search Engine